本記事では、ベクトルで表されたコーシー・シュワルツ不等式の証明を、
- 幾何学的な方法
- 代数的な方法
の2パターンで解説していきます。
もちろん証明だけでは終わらず、その後は、コーシー・シュワルツ不等式から、まず、内積とコサインの関係式を導き、さらには「2つの異なるベクトルの角度」の概念の自然な導出を試みます。
本記事を読むことで、コーシー・シュワルツ不等式の形式的な証明の理解に留まらず、それが、内積や角度の概念と具体的にどう関連してくるのかが分かるはずです。
多変数微積分、ベクトル解析、線形代数などを勉強している方には特に役立つ内容かと思いますので、活用していただけたら幸いです。
コーシー・シュワルツの不等式
ベクトル版コーシー・シュワルツの不等式とは、以下の不等式に関する定理(主張)です。
任意の\(\mathbf{a} ,\mathbf{b} \in \mathbb{R}^n\)について、
\[|\mathbf{a} \cdot \mathbf{b} | \leq \|\mathbf{a} \|\;\|\mathbf{b} \|\]
が成り立つ。
幾何学的な証明
まずは、幾何学的な方法による証明を示します。証明では、射影の概念を活用するので、射影に慣れていない場合は「内積と射影の関係とは？ 〜正規化された方向ベクトルを用いた内積とその解釈・応用例〜」も参考にしてください。
また、この幾何学的な証明にあたっては、まず\( \mathbf{a}, \mathbf{b} \) のうち、\( \mathbf{b} \)を単位ベクトルとする「特別なケース」から始め、その後、一般化するという流れで進めます。
特別なケース
\(\mathbf{a}\)は\(\mathbb{R}^n\)の任意のベクトルです。\(\mathbf{b}\)に関しては、任意の単位ベクトルとして、\(\|\mathbf{b}\| = 1\)を満たすとします。まず、\(c\)を\(\mathbf{b}\)に沿う\(\mathbf{a}\)の成分とすれば、
\[c = \mathbf{a}\cdot \mathbf{b}\]
です。また、\(c\mathbf{b}\)は、\(\mathbf{b}\)に沿う\(\mathbf{a}\)の射影(ベクトル)、\(\mathbf{a} – c\mathbf{b}\)は、\(c\mathbf{b}\)と直交するベクトルです。このとき、
\[\mathbf{a} = (\mathbf{a} – c\mathbf{b}) + c\mathbf{b}\]
なので、
\[\|\mathbf{a}\|^2 = \|(\mathbf{a} – c\mathbf{b}) + c\mathbf{b}\|^2\]
が成り立ちます。\(\mathbf{a} – c\mathbf{b}\)は、\(c\mathbf{b}\)と直交するから、ピタゴラスの定理を適用できて、
\begin{align}
\|\mathbf{a}\|^2 &= \|(\mathbf{a} – c\mathbf{b}) + c\mathbf{b}\|^2 \\
&= \|\mathbf{a} – c\mathbf{b}\|^2 + \|c\mathbf{b}\|^2 \\
&= \|\mathbf{a} – c\mathbf{b}\|^2 + c^2 \\
\end{align}
となります。これより
\[c^2 \leq \|\mathbf{a}\|^2\]
で、両辺の平方根を取れば、\(|c| \leq \|\mathbf{a}\|\)で、\(c = \mathbf{a}\cdot \mathbf{b}\)だから
\[|\mathbf{a}\cdot \mathbf{b}| \leq \|\mathbf{a}\|\]
を得ます。今は、\(\|\mathbf{b}\|=1\)を仮定しているから、この結果を
\[|\mathbf{a}\cdot \mathbf{b}| \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\]
としても意味は変わりません。よって、まずは、\(\|\mathbf{b}\| = 1\)という制約を設けた特別なケースについて目的の不等式が証明されました。
本証明
\(\mathbf{a},\mathbf{b}\in \mathbb{R}^n\)は任意のベクトルとします。\(\mathbf{b}=\mathbf{0}\)のとき、不等式は\(0\leq 0\)として成立します。そこで、以下では\(\mathbf{b} \neq \mathbf{0}\)として進めます。
まずは、1つ前に得た結果\(|\mathbf{a}\cdot \mathbf{b}| \leq \|\mathbf{a}\|\;\;(\mathrm{ただし}\|\mathbf{b}\| = 1)\)を利用するために、\(\mathbf{b}\)を正規化します。正規化した\(\mathbf{b}\)を\(\mathbf{e}_{\mathbf{b}}\)とすれば、
\[\mathbf{e}_{\mathbf{b}} = \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
です。\(|\mathbf{a}\cdot \mathbf{b}| \leq \|\mathbf{a}\|\)の\(\mathbf{b}\)を\(\mathbf{e}_{\mathbf{b}}\)で置き換えることにより、
\[\frac{|\mathbf{a}\cdot\mathbf{b}|}{\|\mathbf{b}\|} \leq \|\mathbf{a}\|\]
です。両辺に、\(\mathbf{b}\)をかけることで、
\[|\mathbf{a} \cdot \mathbf{b} | \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\]
とコーシー・シュワルツの不等式を得ます。
以上が、コーシー・シュワルツの不等式の幾何学的な証明です。次からは、代数的な方法によって不等式を証明していきます。
代数的な証明
\(t\)を任意の実数をとる変数として、関数\(\|t\mathbf{a}+\mathbf{b}\|^2\)を定めます。これに対して、ノルムと内積の性質、2次式の平方完成を用いることで、
\begin{align}
\|t\mathbf{a}+\mathbf{b}\|^2 &= (t\mathbf{a}+\mathbf{b})\cdot(t\mathbf{a}+\mathbf{b})\\
&= t^2 \mathbf{a}\cdot \mathbf{a} + 2t\mathbf{a}\cdot\mathbf{b} + \mathbf{b}\cdot \mathbf{b}\\
&= \left(t\sqrt{\mathbf{a}\cdot \mathbf{a}} + \frac{\mathbf{a}\cdot \mathbf{b}}{\sqrt{\mathbf{a}\cdot \mathbf{a}}}\right)^2 – \frac{(\mathbf{a} \cdot \mathbf{b})^2}{\mathbf{a}\cdot \mathbf{a}} + \mathbf{b}\cdot \mathbf{b}\\
&= \left(t\|\mathbf{a}\| + \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{a}\|}\right)^2 – \frac{(\mathbf{a} \cdot \mathbf{b})^2}{\|\mathbf{a}\|^2} + \|\mathbf{b}\|^2
\end{align}
を得ます。ノルムは非負だから、\(0 \leq \|t\mathbf{a}-\mathbf{b}\|^2\)、つまり、
\[0 \leq \left(t\|\mathbf{a}\| + \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{a}\|}\right)^2 – \frac{(\mathbf{a} \cdot \mathbf{b})^2}{\|\mathbf{a}\|^2} + \|\mathbf{b}\|^2\]
で、特に、\(t = -(\mathbf{a}\cdot \mathbf{b})/\|\mathbf{a}\|^2\)のとき、
\[0 \leq – \frac{(\mathbf{a} \cdot \mathbf{b})^2}{\|\mathbf{a}\|^2} + \|\mathbf{b}\|^2\]
です。これを移項や平方根をとるなどの整理すれば、目的の不等式が得られます。
以上がコーシー・シュワルツ不等式の代数的な証明となります。以降では、引き続き、代数的な方法を用いて、不等式の等号成立条件を見ていきます。
等号成立の必要十分条件
コーシー・シュワルツ不等式の統合成立条件は、以下の定理としてまとめられます。
コーシー・シュワルツの不等式の等号成立の必要十分条件は、\(\mathbf{a}\)と\(\mathbf{b}\)が線形従属になること。つまり、ある実数\(t\)が存在して、
\[ \mathbf{b} = t \mathbf{a}\]
が成り立つことである。
それでは、不等式の等号成立条件を証明していきます。必要十分条件なので、必要性と十分性の2つを証明します。
\(|\mathbf{a} \cdot \mathbf{b}| = \|\mathbf{a}\|\;\|\mathbf{b}\|\)が成り立つと仮定します。先ほどと同様に、\(t\)を実数を変域とする変数として、関数\(\|t\mathbf{a}+\mathbf{b}\|^2\)を定めると、
\[\|t\mathbf{a}+\mathbf{b}\|^2 = t^2\|\mathbf{a}\|^2 + 2t \mathbf{a}\cdot \mathbf{b} + \|\mathbf{b}\|^2\]
であり、仮定より、\(\|\mathbf{b}\| = |\mathbf{a} \cdot \mathbf{b}| / \|\mathbf{a}\|\)だから、これを上式の\(\|\mathbf{b}\|\)に代入すれば
\begin{align}
\|t\mathbf{a}+\mathbf{b}\|^2 &= t^2\|\mathbf{a}\|^2 + 2t \mathbf{a}\cdot \mathbf{b} + \left(\frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{a}\|}\right)^2\\
&= \left(t\|\mathbf{a}\| + \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{a}\|}\right)^2
\end{align}
を得ます。さらにノルムは非負だから、
\[0 \leq \left(t\|\mathbf{a}\| + \frac{\mathbf{a}\cdot \mathbf{b}}{\|\mathbf{a}\|}\right)^2\]
である。ここで、変数\(t\)に、\(t^\ast = -(\mathbf{a}\cdot \mathbf{b})/\|\mathbf{a}\|^2\)として代入すれば
\[\|t^\ast \mathbf{a}+\mathbf{b}\|^2 = 0\]
であり、ノルムの性質から、
\[t^\ast \mathbf{a} + \mathbf{b} = \mathbf{0}\]
すなわち、\(\mathbf{b} = -t^\ast \mathbf{a}\)。これより、\(\mathbf{b} = t\mathbf{a}\)を満たす\(t\)の存在が確かめられました。
ある実数\(t\)が存在して、\(\mathbf{b}=t\mathbf{a}\)が成り立つと仮定します。このとき、両辺に\(\mathbf{a}\)での内積の絶対値をとれば、
\[|\mathbf{a}\cdot \mathbf{b}| = |t|\;|\mathbf{a}\cdot\mathbf{a}| = |t|\|\mathbf{a}\|^2\]
です。他方、\(\|\mathbf{b}\| = |t|\;\|\mathbf{a}\|\)より、\(|t|=\|\mathbf{b}\|/\|\mathbf{a}\|\)だから、これを上式の\(|t|\)に代入することで、
\[|\mathbf{a}\cdot \mathbf{b}| = \|\mathbf{a} \|\;\|\mathbf{b}\|\]
を得ます。
「角度」の導入と正規化されたベクトルどうしの内積
任意のベクトル\(\mathbf{a},\mathbf{b}\)に関するコーシー・シュワルツの不等式は
\[|\mathbf{a}\cdot \mathbf{b}| \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\]
ですが、これを絶対値を使わずに表すと、
\[-\|\mathbf{a}\|\;\|\mathbf{b}\| \leq \mathbf{a}\cdot \mathbf{b} \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\]
です。この表現により、まず内積\(\mathbf{a}\cdot \mathbf{b}\)の上限値・下限値がより明確になります。
なお、ここでの「上限・下限」という用語は、順序関係に基づく厳密な意味ではなく、今これを読んでいるあなたの直感に依存するラフな使い方をしています。
さらに、両辺を\(\|\mathbf{a}\|\;\|\mathbf{b}\|\)で割れば、
\[-1 \leq \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|} \leq 1\]
となります。ここで、
\[\frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
は、正規化された、つまり、ノルム(大きさ)が1の\(\mathbf{a}\)と\(\mathbf{b}\)の内積であることに注意しましょう。その上で、この内積は、-1以上1以下の範囲の値に収まることが分かります。ところで、\(-1 \leq \cos \theta \leq 1\)でもあるので、
\[\cos \theta = \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
という等式が成立します。この等式は、内積という代数的な演算とコサインという幾何学的な概念を結び付けています。
この等式において、\(\theta\)の取り得る範囲を\(0 \leq \theta \leq \pi\)と制限すれば、正規化されたベクトル\(\mathbf{a},\mathbf{b}\)の内積から、\(\theta\)がただ一つ定まります。
つまり、正規化された\(\mathbf{a}\)と\(\mathbf{b}\)の内積は、\(\cos \theta\)の逆関数であり、この\(\theta\)を「\(\mathbf{a}\)と\(\mathbf{b}\)の間の角度」として定義します。
これにより、「正規化されたベクトルどうし」の内積の意義がより明確になります。つまり、「正規化されたベクトルどうし」の内積とは、2つの異なるベクトル\(\mathbf{a}\)と\(\mathbf{b}\)の「(相対的な)方向関係とその度合い」を算出するツールです。
具体的に見ていきましょう。正規化された\(\mathbf{a}\)と\(\mathbf{b}\)の内積の値、つまり\(\cos \theta\)は、角度\(\theta\)と1対1で紐づいているので、\(\mathbf{a}\)と\(\mathbf{b}\)の相対的な位置関係とその程度(開き具合)を、前者は-1以上1以下で、後者は\(0 \leq \theta \leq \pi\)の範囲で表します。
以下の表では、\(\mathbf{a}\)と\(\mathbf{b}\)の方向関係を、\(\cos \theta\)と\(\theta\)に基づき、便宜的に3パターンに分類しています。
\( \cos \theta\) 、\( \theta\)、\( \mathbf{a} \) と\( \mathbf{b} \)の方向関係の対応関係以下では、これら３パターンの関係性をより詳しくみていきます。
「同じ」方向の関係性とその程度
正規化された\(\mathbf{a},\mathbf{b}\)の内積の値(\(= \cos \theta\))が、0より大きく1以下のとき、または、\(\mathbf{a},\mathbf{b}\)の間の角度\(\theta\)が\(0 \leq \theta \leq \pi/2\)の範囲にあるとき、2つのベクトル\(\mathbf{a}\)と\(\mathbf{b}\)は、「同じ」方向の関係性です。
このとき、\(\cos \theta\)(内積の値)が\(1\)に近づくことに連動して、角度\(\theta\)が\(0\)に近づくことで、\(\mathbf{a}\)と\(\mathbf{b}\)の「同じ」方向の関係性は強まります。
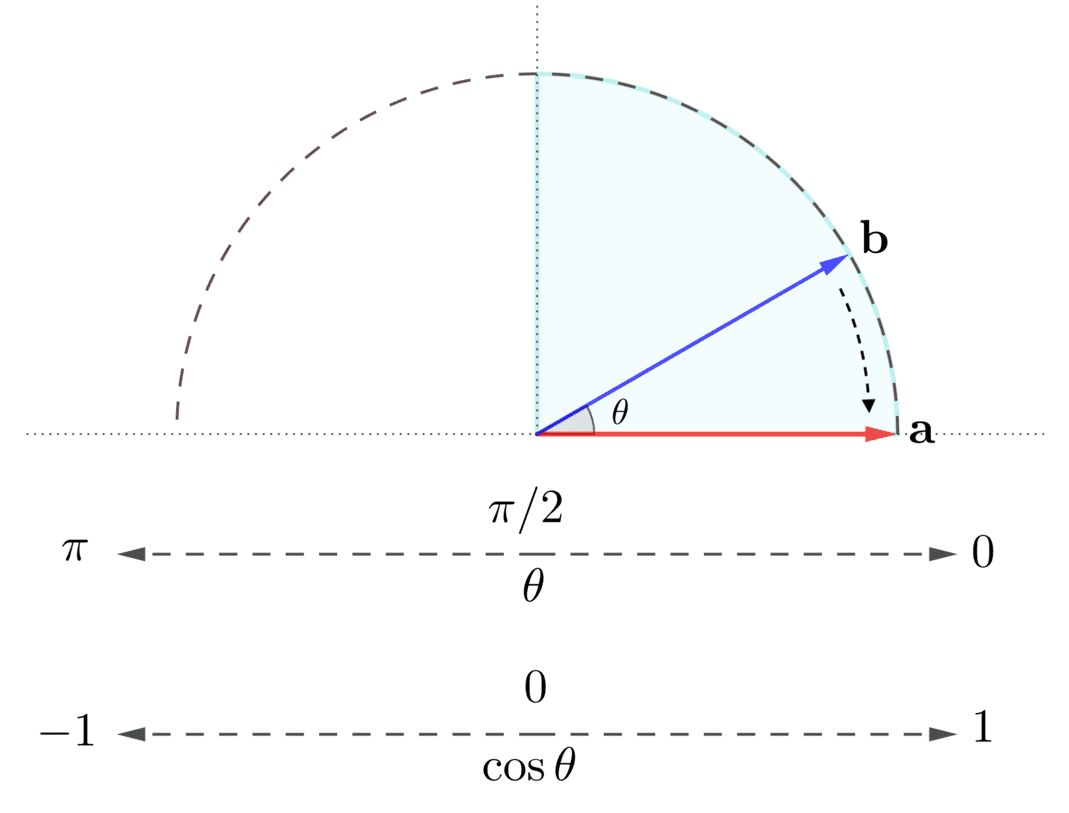水色で塗った領域で、\(\mathbf{a} \) と\( \mathbf{b} \) は「同じ」方向の関係性
最終的に、\(\cos \theta = 1\)、つまり、\(\mathbf{a}\)と\(\mathbf{b}\)の間の角度が\(0\)になったとき、\(\mathbf{a},\mathbf{b}\)は、完全な同じ方向の関係性になります。
このことを、これまでの内容をもとにより厳密に表現するらな、
\[\cos \theta = 1 = \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
より、
\[\mathbf{a}\cdot \mathbf{b} = \|\mathbf{a}\|\;\|\mathbf{b}\|\]
となり、コーシー・シュワルツ不等式において等号が成立し、ある実数\(0 < t\)が存在して、\(\mathbf{b} = t \mathbf{a}\)、すなわち、\(\mathbf{a},\mathbf{b}\)は線形従属の関係ということになります。
「反対」方向の関係性とその度合い
正規化された\(\mathbf{a},\mathbf{b}\)の内積の値(\(= \cos \theta\))が、-1以上0未満のとき、または、\(\mathbf{a},\mathbf{b}\)の間の角度\(\theta\)が\(\pi/2 \leq \theta \leq \pi\)の範囲にあるとき、2つのベクトル\(\mathbf{a}\)と\(\mathbf{b}\)は、「反対」方向の関係性です。
このとき、\(\cos \theta\)(内積の値)が\(-1\)に近づくことに連動して、角度\(\theta\)が\(\pi\)に近づくことで、\(\mathbf{a}\)と\(\mathbf{b}\)の「反対」方向の関係性は強まります。
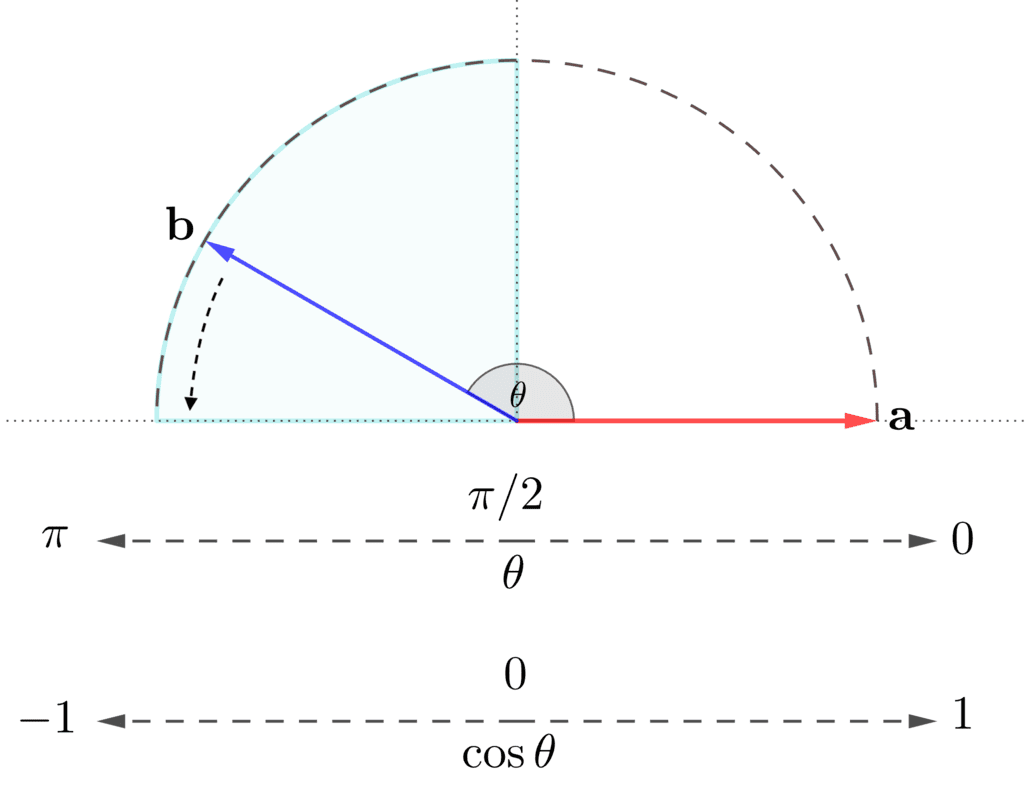水色で塗った領域で、\(\mathbf{a} \) と\( \mathbf{b} \) は「反対」方向の関係性
最終的に、\(\cos \theta = -1\)、つまり、\(\mathbf{a}\)と\(\mathbf{b}\)の間の角度が\(\pi\)になったとき、\(\mathbf{a},\mathbf{b}\)は、完全な反対方向の関係性になります。\\
これをより厳密に表現するなら、
\[\cos \theta = -1 = \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
より、
\[\mathbf{a}\cdot \mathbf{b} = -\|\mathbf{a}\|\;\|\mathbf{b}\|\]
となり、コーシー・シュワルツ不等式において等号が成立し、ある実数\(t < 0\)が存在して、\(\mathbf{b} = t \mathbf{a}\)、すなわち、\(\mathbf{a},\mathbf{b}\)は線形従属の関係となります。
「直交」の関係性とその程度
正規化された\(\mathbf{a},\mathbf{b}\)の内積の値(\(= \cos \theta\))が、\(0\)のとき、または、\(\mathbf{a},\mathbf{b}\)の間の角度\(\theta\)が\(\pi/2\)のとき、2つのベクトル\(\mathbf{a}\)と\(\mathbf{b}\)は、「直交」の関係性、すなわち、「(線形的に)無関係」です。
このとき、\(\mathbf{a}\)と\(\mathbf{b}\)が、「同じ」、「反対」いずれの関係性であったとしても、\(\cos \theta\)(内積の値)が\(0\)に近づくことに連動し、角度\(\theta\)は\(\pi/2\)に近づき、\(\mathbf{a}\)と\(\mathbf{b}\)は直交関係に近づき、従って、(線形的な)両者の関係性は薄まっていきます。
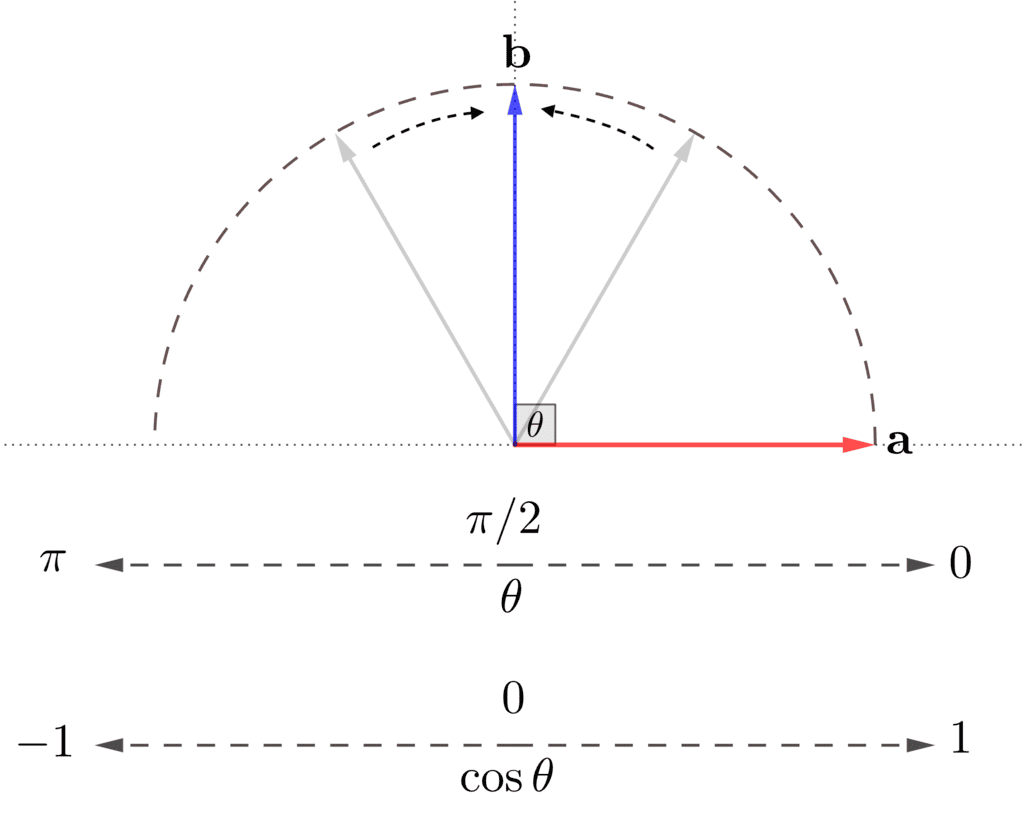\(\theta = \pi/2 \) に近づくにつれ、\( \mathbf{a} \) と\( \mathbf{b} \) は「直交」関係に近づく
最終的に、\(\cos \theta = 0\)、つまり、\(\mathbf{a}\)と\(\mathbf{b}\)の間の角度が\(\pi/2\)になったとき、\(\mathbf{a},\mathbf{b}\)は、直交関係になります。これをより厳密に表現するなら、
\[\cos \theta = 0 = \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
より、
\[\mathbf{a}\cdot \mathbf{b} = 0\]
となり、\(\mathbf{a}\)と\(\mathbf{b}\)の内積の値は0になります。
「角度」を導入することの意義 〜方向関係という新たな視点〜
ここまで見てきたように、正規化されたベクトルどうしの内積をコサインと結びつける、つまり、「角度」の導入することで、2つの異なるベクトルの
- 相対的な方向関係・位置関係
- その度合い・程度
把握できるようになります。
ベクトルの「方向」という概念は、ベクトルそのものを特徴づけていて、「角度」を導入する前から定まっています。
しかし、「角度」を導入することで、個々のベクトル1つ1つの「向き」を超えて、２つのベクトルの「方向関係とその関係の度合い」を扱えるようになるわけです。
「方向」と「方向関係」は似ていますが、明確に異なる概念なので混同しないようにしましょう。
- 方向：単体のベクトルが持つ向きで、始点を原点に置いたときの終点の座標として数値化される
- 方向関係(角度)：2つのベクトルの位置関係・向きの関係
なお、ベクトルの方向に関しては、『3次元空間における「ベクトル」という概念とその本質: 空間の点、順序対、有向線分の統一的な理解』で解説しているので参考にして下さい。
内積の注意点と角度との関連
\(\mathbf{a}\)と\(\mathbf{b}\)がともに正規化されているとき、これらの内積は、「\(\mathbf{a}\)と\(\mathbf{b}\)の方向関係とその度合いを算出する」ツールです。
では、\(\mathbf{a}\)と\(\mathbf{b}\)がともに正規化されていないケースの内積に対しては、どのような意味付けや解釈ができるのでしょうか？そこで、以下では、
- \(\mathbf{a},\mathbf{b}\)両方とも正規化されていない内積
- \(\mathbf{a},\mathbf{b}\)の一方だけ正規化されている内積
を考察することで、内積を扱う際の注意点やコツを確認していきます。
\(\mathbf{a},\mathbf{b}\)両方とも正規化されていない内積
等式
\[\cos \theta = \frac{\mathbf{a}}{\|\mathbf{a}\|}\cdot \frac{\mathbf{b}}{\|\mathbf{b}\|}\]
に対して、両辺\(\|\mathbf{a}\|\;\|\mathbf{b}\|\)をかければ、
\[\mathbf{a}\cdot \mathbf{b} = \|\mathbf{a}\|\;\|\mathbf{b}\|\cos \theta\]
と、\(\mathbf{a},\mathbf{b}\)両方とも正規化されていない内積が得られます。右辺に関して、\(0 \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\)だから、内積\(\mathbf{a}\cdot \mathbf{b}\)の符号は、\(\cos \theta\)の符号と直接対応しています。
以下の表のように、\(\cos \theta\)の符号は、\(\mathbf{a}\)と\(\mathbf{b}\)の方向関係3パターンに対応するから、
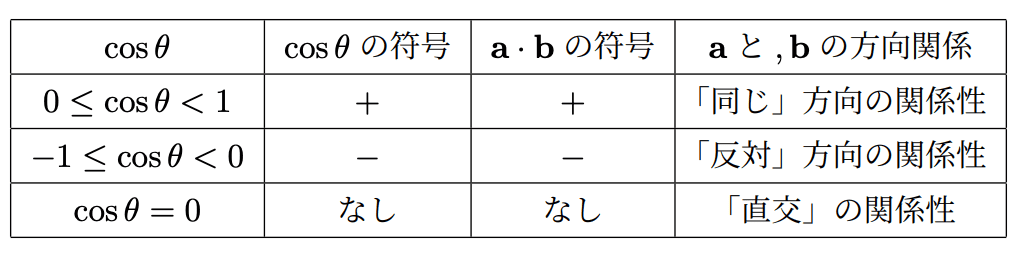
\( \cos \theta\) の符号と\( \mathbf{a} \) と\( \mathbf{b} \)の方向関係\(\mathbf{a},\mathbf{b}\)両方とも正規化されていない内積は、その符号を、\(\mathbf{a}\)と\(\mathbf{b}\)の方向関係の3パターンの指標として使えます。
ただし、この場合、内積の絶対値には実質的な意味を付与するのは難しくなります。つまり、「方向関係の強さ(程度)」の指標としては使いづらいです。なぜなら、先に見たように、
\[-\|\mathbf{a}\|\;\|\mathbf{b}\| \leq \mathbf{a}\cdot \mathbf{b} \leq \|\mathbf{a}\|\;\|\mathbf{b}\|\]
であり、内積\(\mathbf{a}\cdot \mathbf{b}\)は、、\(\mathbf{a}\)と\(\mathbf{b}\)のノルム\(\|\mathbf{a}\|\;\|\mathbf{b}\|\)を反映してしまうからです。\\
特に、\(\mathbf{c}\)という第３のベクトルを持ってきて、\(\mathbf{b}\)と\(\mathbf{c}\)いずれも、\(\mathbf{a}\)と「同じ」方向の関係性にあるとき、どちらがより強い「同じ」方向の関係性にあるかの指標に正規化されていない内積\(\mathbf{a}\cdot \mathbf{b}\)と\(\mathbf{a}\cdot \mathbf{c}\)を比較してもそれは意味がありません。
\(\mathbf{b}\)だけ正規化されている内積
任意の2つのベクトル\(\mathbf{a},\mathbf{b}\)に対して、\(\mathbf{b}\)が正規化されている(\(\|\mathbf{b}\|=1\))のケースでの内積は、『内積と射影の関係とは？ 〜正規化された方向ベクトルを用いた内積とその解釈・応用例〜』で解説している通り、幾何学的には\(\mathbf{b}\)に沿う\(\mathbf{a}\)の射影として、\(\mathbf{b}\)方向に対する\(\mathbf{a}\)の影響力・寄与度の指標として解釈できます。
共分散と相関係数
正規化された2つのベクトルの内積(またはコサイン)の応用例として、統計学における相関係数があります。詳しくは「多変量データの行列・ベクトル表現と導出 〜多変量データ行列から分散共分散行列まで〜」で解説しています。
また、相関係数との直接の関連として、’正規化されていない’２つのベクトルの内積は、共分散に対応します。
統計学の文脈で共分散を習うとき、「共分散の値そのものには意味がない」ということを教わります。
これは、本記事で散々解説したように、2つのデータベクトル（正確には「平均偏差ベクトル」）のノルムが1ではないために、データベクトルに内在する「単位」次第で、共分散の値が大きくも小さくもなりうるからです。
参考文献
本記事を執筆するにあたり参考にした書籍・教材は以下の通りです。
なお、参考文献や教材の紹介にあたっては、アフィリエイトリンクを貼っていることをご承知ください。
ラング 続解析入門
コーシー・シュワルツ不等式の幾何学的な証明は本書をもとにしました。
物理数学、経済数学の入門書として最適です。
計量経済学のための数学
コーシー・シュワルツ不等式の代数的な証明は本書をもとにしました。
計量経済学（統計学）に最低限必要な内容を厳選して、線形代数と(やや高度な）確率論を学ぶことができます。
線形代数の理論とPythonによる実践
線形代数の理論とPythonによる実践は、本ではなくUdemyの動画教材です。
本記事では、コーシー・シュワルツ不等式から、内積とコサインの等式を導き、角度を導入するという一連の流れを参考にしました。
