この記事では、多変数微積分、ベクトル解析、線形代数などで基本かつ重要な概念である
- 空間の点
- 実数の順序対
- 有向線分(空間の中にある矢印)
という3つの異なる概念が、「向き」と「大きさ」という観点で相互の関連性に着目することで、実際には互いが1対1に対応していて、「ベクトル」という1つの概念で統一的に捉えられることを図を用いながら丁寧に解説していきます。
この記事は以下のような方に特に最適です。
- 多変数微積分やベクトル解析を学んでいて、空間の点と有向線分の関係性をより明確に理解したい人
- 線形代数を学び始めて「ベクトル」と連呼される割には、抽象的な数のリストばかりで慣れ親しんだ「有向線分(矢印)」としてのベクトルとの関連に戸惑っている人
記事内では、3次元空間を具体例として解説していきますが、この記事の内容を理解できれば、n次元への拡張は容易にできるようになるはずです。
また本記事では、「向き」と「大きさ」という観点から、空間の点、順序対、有向線分を「ベクトル」という概念で抽象化していきますが、これ以上の抽象化には立ち入りません。
空間の点と順序対
以下の3次元空間を考えます。
この3次元空間には、3本の座標軸と原点\(\mathbf{0}\)が導入されています。従って、空間内の点を適当に1つ指定すると、この点は3つの数の組
\[(p_1,p_2,p_3)\]
で表すことができます。この数の組を、この点の「座標」というのでした。

逆に、\(p_i\)を1つの数とし、これを3つ集めてできる数の組\((p_1,p_2,p_3)\)を定めれば、これは3本の座標軸が導入された3次元空間の1つの点に対応します。
このように、3次元空間の「1つの点」は、座標軸と座標を介して「3つの数の組」と1対1に対応します。ただし、「3つの数の組」とは、「3つの数の順序を考慮した組」であるとし、以降では「(3つの数の)順序対」と呼ぶことにします。
\((p_1,p_2,p_3)\)を構成する\(p_i\)は「実数」を想定します。すると、「実数全体の集合」を\(\mathbb{R}\)としたとき、\(p_i\)は\(\mathbb{R}\)の中の1つの要素になります。これは、
\[p_i \in \mathbb{R}\]
と表されます。よって、3つの数の順序対\((p_1,p_2,p_3)\)は、3つの実数の順序対全体の中の1つとみなせます。この順序対全体は、実数全体の集合\(\mathbb{R}\)を3つ用いて構成されるので、これを
\[\mathbb{R}^3\: \mathrm{または}\: \mathbb{R} \times \mathbb{R} \times \mathbb{R}\]
と表し、正式には「3つの実数集合の直積」と言います。
ここまでをまとめましょう。まず、3次元空間の点は、3つの実数の順序対と等価です。つまり、
\[\mathrm{3次元空間の1つの点} \leftrightarrow (p_1,p_2,p_3)\]
です。これより、3次元空間は、実数全体の集合\(\mathbb{R}\)の3つの直積と等価です。つまり、
\[\mathrm{3次元空間} \leftrightarrow \mathbb{R}^3\]
です。従って、
- 3次元空間の中の1つの点
- 3つの実数の順序対全体の中の1つの要素
は、表面上は異なる表現ですが、
\[(p_1, p_2, p_3) \in \mathbb{R}^3\]
という1つの概念を異なる視点から捉えたものと理解できます。\(\mathbf{p} = (p_1, p_2, p_3)\)とすれば、
\[\mathbf{p} \in \mathbb{R}^3\]
となります。なお以降では、順序対\(\mathbf{p}=(p_1,p_2,p_3)\)の表し方に関して、
\[\mathbf{p} = \begin{pmatrix}p_1\\ p_2\\ p_3\end{pmatrix}\]
という縦(列)表記をデフォルトとします。これは、本ブログの全ての記事との整合性を保つためです。
より詳しく言えば、ユーグリッド空間での内積(スカラー積)や行列によって表された線形写像の導入の際に、記法の断りや修正の煩雑さを無くすためです。
ただし、この縦表記だと、インラインに組み込めなくなるので、転置記号\(\top\)を用いて、
\[\mathbf{a} = \begin{pmatrix}p_1\\ p_2\\ p_3\end{pmatrix}=(p_1,p_2,p_3)^\top\]
という形で、列(縦)表記をすることも多々あります。
定置ベクトル (有向線分)
このセクションは、次のセクションの「準備」のような位置づけとなります。よく知られた「空間内の矢印/有向線分」を導入して、その性質を考察していきます。ここでの論点は、
- 2つの有向線分が等しいことはどう定義されるのか?
- この定義は何を意味しているのか?
という2点です。
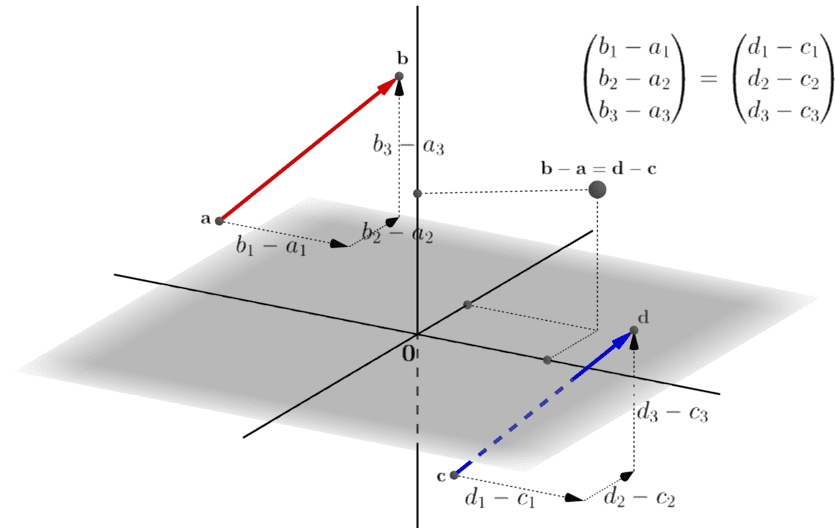
\(\mathbb{R}^3\)の異なる2つの点\(\mathbf{a},\mathbf{b}\)を任意に選び、「\(\mathbf{a}\)から\(\mathbf{b}\)へ」という「方向」のある2点間の有向線分を考えます。

この有向線分を\(\overrightarrow{\mathbf{ab}}\)で表し、「定置ベクトル」と呼ぶことにします。\(\mathbf{a}\)は定置ベクトルの始点、\(\mathbf{b}\)は終点です。なお、定置ベクトルという呼び方は、本記事の参考文献「ラング 続解析入門」に倣っています。
まず、2つの任意の定置ベクトル\(\overrightarrow{\mathbf{ab}},\; \overrightarrow{\mathbf{cd}}\)に対して、これらが等しいことは、
\[\mathbf{b} – \mathbf{a} = \mathbf{d} – \mathbf{c}\]
が成り立つこと、と定義されます。このセクションの目的は、この意味を理解することです。まず、
\[\mathbf{b} – \mathbf{a}\]
ですが、これは定置ベクトル\(\overrightarrow{\mathbf{ab}}\)の終点\(\mathbf{b}\)と始点\(\mathbf{a}\)の差分をとっています。\(\mathbf{a},\mathbf{b}\)の座標を、\(\mathbf{a} = (a_1,a_2,a_3)^\top\)、\(\mathbf{b} = (b_1,b_2,b_3)^\top\)とすれば、
\[\mathbf{b} – \mathbf{a}= \begin{pmatrix}b_1 – a_1\\ b_2 – a_2\\ b_3 – a_3\end{pmatrix}\]
ということです。
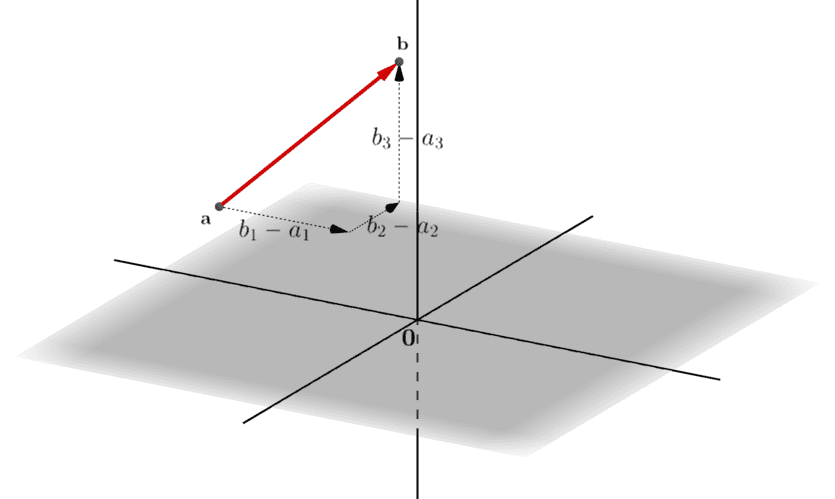
これは、始点\(\mathbf{a}\)から終点\(\mathbf{b}\)への「移動方向」と「移動量」を、
- \(\mathbf{a}\)と\(\mathbf{b}\)の対応する座標成分の差\(b_i – a_i\)として各軸ごとに取得し、
- 全体として3つの実数の順序対\((b_1 – a_1,\;b_2 – a_2,\; b_3 – a_3)^\top \)として定め直す
操作と解釈できます。
すなわち、定置ベクトル\(\overrightarrow{\mathbf{ab}}\)が、\(\mathbf{R}^3\)の「どこに位置するか」という「位置」情報を捨て去り、\(\overrightarrow{\mathbf{ab}}\)の「向き」と「大きさ」に関する情報のみを抽出し、これを\(\mathbb{R}^3\)の1つの点\(\mathbf{b}-\mathbf{a}\)で表し直しています。
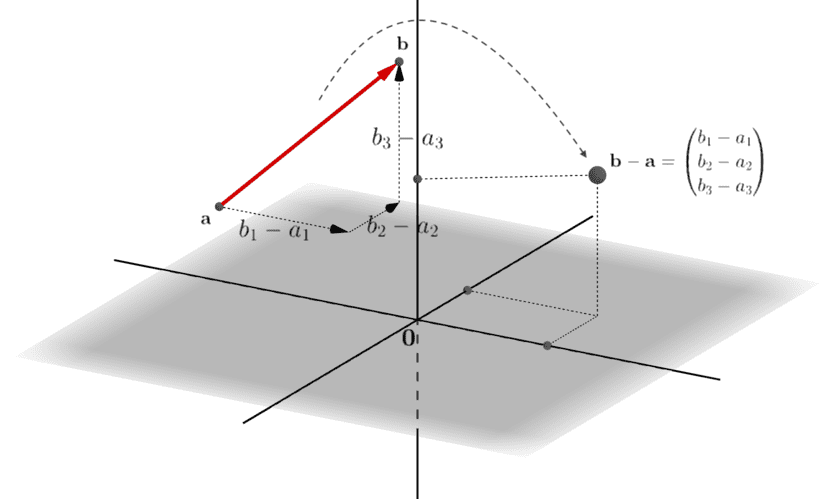
\(\overrightarrow{\mathbf{cd}}\)についても同様です。つまり、始点\(\mathbf{c} = (c_1,c_2, c_3)^\top\)から終点\(\mathbf{d}=(d_1,d_2, d_3)^\top\)への移動方向と移動量を、各軸ごとに\(d_i – c_i\)として取得し、全体として
\[\mathbf{d} – \mathbf{c}= \begin{pmatrix}d_1 – c_1\\ d_2 – c_2\\ d_3 – c_3\end{pmatrix}\]
というように\(\mathbf{R}^3\)の1つの点\(\mathbf{d}-\mathbf{c}\)として表し直します。
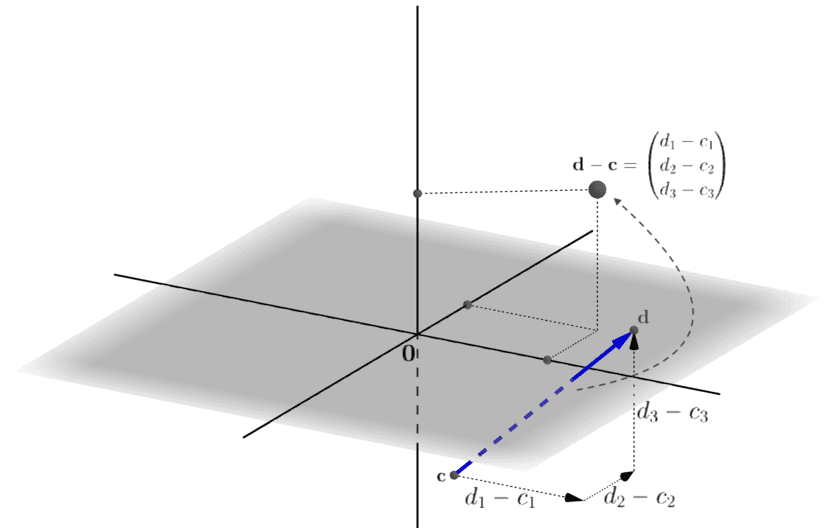
このとき、\(\mathbf{b} – \mathbf{a}\)と\(\mathbf{d} – \mathbf{c}\)が、同じ\(\mathbb{R}^3\)の点を表すなら、すなわち、それぞれの「移動方向(向き)」と「移動量(大きさ/長さ)」が同じであるとき、\(\overrightarrow{\mathbf{ab}}\)と\(\overrightarrow{\mathbf{cd}}\)は「等しい」とされるわけです。
ベクトルの同値性をこのように定義するのは、ベクトルの本質が、その「向き」と「大きさ」だけにあることを意味しています。つまり、「向き」と「大きさ」が同じベクトルなら、どこに位置しようとも、同じベクトルとして扱うことです。
「ベクトル」という概念による統一的な理解
このセクションでは、まず最初に、1つ前のセクションをもとに、\(\mathbb{R}^3\)の点と定置ベクトルを対応関係を見ていきます。その上で、「ベクトル」という1つの概念で、
- 空間の点
- 始点が原点の定置ベクトル
- 順序対
という3つの異なる概念が互いに1対1に対応していることを確認していきます。
任意の定置ベクトル\(\overrightarrow{\mathbf{ab}}\)に対して、これと同値な始点が原点\(\mathbf{0}\)の定置ベクトルとして、
\[\overrightarrow{\mathbf{0(b-a)}}\]
がただ1つ定まります。この定置ベクトルの終点は\(\mathbf{b}-\mathbf{a}\)です。幾何学的に、これは\(\overrightarrow{\mathbf{ab}}\)を、その向きと大きさは保ったまま、始点を原点\(\mathbf{0}\)にする「平行移動」に相当します。

先に見たように、点\(\mathbf{b}-\mathbf{a}\)は、\(\overrightarrow{\mathbf{ab}}\)の終点\(\mathbf{b}\)と始点\(\mathbf{a}\)の差分として、\(\overrightarrow{\mathbf{ab}}\)の「位置」情報を削ぎ落とし、\(\overrightarrow{\mathbf{ab}}\)の「向き」と「大きさ」に関する情報のみを順序対として表した\(\mathbb{R}^3\)の1つの点です。
よって、任意の定置ベクトル\(\overrightarrow{\mathbf{ab}}\)を始点が\(\mathbf{0}\)の同値な定置ベクトルに変換することは、
- 「向き」と「大きさ」という定置ベクトル\(\overrightarrow{\mathbf{ab}}\)の本質的な性質のみを順序対\(\mathbf{b}-\mathbf{a}\)として抽出して、
- それを空間の1点\(\mathbf{b}-\mathbf{a}\)として表現し直す
操作ということになります。このとき、この空間の1点\(\mathbf{b}-\mathbf{a}\)は、終点と始点の差分がこの点の座標に一致する全ての定置ベクトルを代表しています。
以上に基けば、\(\mathbb{R}^3\)の任意の点の座標は、始点が原点\(\mathbf{0}\)、終点がその点の定置ベクトルの「向き」と「大きさ」を表していると言えます。
すなわち、\(\mathbb{R}^3\)の1つの点とは、原点\(\mathbf{0}\)を基準点として、その点が原点\(\mathbf{0}\)から「どの方向」に「どれだけ離れている」かという特徴付けにより、始点が原点\(\mathbf{0}\)、終点がその点の定置ベクトルそのものと言える。
他方、始点が原点\(\mathbf{0}\)の定置ベクトルは終点により完全に決定されます。従ってこれら2つはに1対1に対応し、同一視が可能です。
以上より、「ベクトル」という数学的概念を、これを\(\mathbf{x}\)として、
- \(\mathbb{R}^3\)の点\(\mathbf{x}\)で、その座標は\((x_1,x_2,x_3)\)
- 始点が原点\(\mathbf{0}\)、終点が\(\mathbf{x}\)の定置ベクトル
- 3つの実数の順序対\(\mathbf{a}=(x_1,x_2,x_3)^\top\)
という3つの異なる数学的対象を統一的に表すものとして定めることができます。
参考文献
本記事を執筆するにあたり「ラング 続解析入門」p1~10を参考にしました。
本書は、多変数微積分とベクトル解析を統一的に扱っているのが特徴で、物理数学や経済数学を学びたい人には特におすすめです。



