本記事では、【ラング 続解析入門】~4章: 合成微分律と勾配ベクトル-4節: 原点からの距離のみに依存する関数~ において、この節の演習問題6 (p95) を取り上げ解説していきます。
この問題自体は、ごく普通の問題です。しかし、少し突っ込んで考えてみると、幾何学的に興味深い事実に気が付いたので本記事で共有します。
【ラング 続解析入門】を持っている人にはもちろんのこと、持っていない人にも話を追えるように書いたつもりなので、興味があれば目を通して頂けると嬉しいです。
問題と解答
まずは、当該の問題を解説します。次のセクションで、この問題から得た学び・気付きを共有します。
\( \mathbf{p},\; \mathbf{q}\) を \(\mathbf{p} = – \mathbf{q} \) を満たす2つの単位ベクトルとする。このとき、原点を中心とする半径1の球面上に \(\mathbf{p} \) と \( \mathbf{q} \) を結ぶ微分可能な曲線が存在することを示せ。なお、\(\mathbf{p} \) に直交する単位ベクトル\( \mathbf{a} \) を仮定してもよい。
『s.ラング 続解析入門p95』より引用
曲線\( \mathbf{c}(t) \) を以下の通り定める。
$$
\mathbf{c}(t) = \cos(t) \mathbf{p} + \sin(t) \mathbf{a}
$$
ここで、\( \mathbf{p} \) と\( \mathbf{a} \) は直交していて、両方のノルムが1であるとする。つまり、
$$
\begin{cases}
\mathbf{p} \cdot \mathbf{a} = 0\\
\|\mathbf{p} \| = \|\mathbf{a} \| = 1\\
\end{cases}
$$
を満たす。まず、この曲線 \(\mathbf{c}(t)\) は、\(t=0\) で \(\mathbf{c}(0) = \mathbf{p}\) であり、\(t=\pi\) で \(\mathbf{c}(\pi) = -\mathbf{p} = \mathbf{q}\) だから、点 \(\mathbf{p}\) と点 \(\mathbf{q}\) を通る。また、\(0 \leq t \leq \pi\) では、\(\mathbf{c}(t) \neq \mathbf{0}\) だから、点 \(\mathbf{p}\) と点 \(\mathbf{q}\) を結ぶ曲線でもある。
次に、この \(\mathbf{c}(t)\) が、単位球面上にあることを確認する。これは、\(\mathbf{c}(t)\) が任意の \(t \: (0 \leq t \leq \pi)\) で \(\|\mathbf{c}(t)\| = 1\) であるかを確認すればよい。
$$
\begin{align*}
\|\mathbf{c}(t)\| &= \sqrt{\mathbf{c}(t)\cdot \mathbf{c}(t)}\\
&= \sqrt{(\cos(t) \mathbf{p} + \sin(t) \mathbf{a})\cdot (\cos(t) \mathbf{p} + \sin(t) \mathbf{a})}\\
&= \sqrt{\cos^2(t)\mathbf{p}\cdot \mathbf{p} + \sin^2(t)\mathbf{a} \cdot \mathbf{a}}\\
&= \sqrt{\cos^2(t) + \sin^2(t)} \\
&= 1
\end{align*}
$$
以上より、\( \mathbf{c}(t)\) が単位球面上にあることが確かめられた。また、\(\mathbf{c}(t)\) の速度ベクトル(接ベクトル) \(\mathbf{c}'(t)\) は、
$$
\mathbf{c}'(t) = -\sin(t)\mathbf{p} + \cos(t)\mathbf{a}
$$
である。これより、\(\mathbf{c}(t)\) が \(0 \leq t \leq \pi\) で微分可能であることがわかる。以上より、原点を中心とする半径1の球面上において、点 \(\mathbf{p}\) と点 \(\mathbf{q}\) を結ぶ微分可能な曲線の存在が確認できた(図1)。
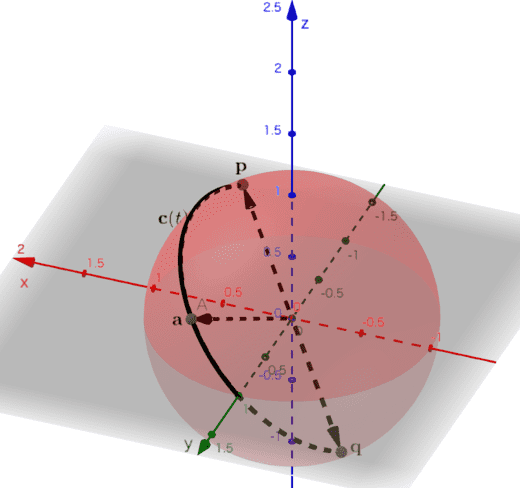 (図1) 黒の曲線が、単位球面上の\( \mathbf{p} \)と\( \mathbf{q} \)を結ぶ曲線\( \mathbf{c}(t) \)
(図1) 黒の曲線が、単位球面上の\( \mathbf{p} \)と\( \mathbf{q} \)を結ぶ曲線\( \mathbf{c}(t) \)
考察と解釈
ここからは、この問題から得られる(少なくとも自分にとっては)興味深い幾何学的な事実があったので、これを紹介していきます。
まず結論から言うと、今求めた曲線\(\mathbf{c}(t)\)ですが、これは、単位球面と2つのベクトル \(\mathbf{p}, \mathbf{a}\) が張る平面の交線になっています。
それでは、このことを確認していきましょう。
まず、\(\mathbf{p}\) と \(\mathbf{a}\) は直交しているので線形独立です。よって、\(\mathbf{p}\) と \(\mathbf{a}\) は、\(\mathbb{R}^3\) の2本の基底として2次元部分空間を生成します。幾何学的に、これは \(\mathbb{R}^3\) 内の原点を通る平面です。
このとき、この平面内の任意のベクトル \(\mathbf{x}\) は、ある係数 \(c_1\) と \(c_2\) が存在して、\(\mathbf{p}\) と \(\mathbf{a}\) の線形結合として一意に表されます。
\[
\mathbf{x} = c_1 \mathbf{p} + c_2 \mathbf{a}
\]
ここで、\(\mathbf{c}(t) = \cos(t) \mathbf{p} + \sin(t) \mathbf{a}\) も、\(\mathbf{p}\) と \(\mathbf{a}\) の線形結合で表されているので、\(\mathbf{p}\) と \(\mathbf{a}\) が生成する平面内の曲線です。すなわち、
$$
\mathbf{c}(t) \in \mathrm{Span}[\mathbf{p}, \mathbf{a}]
$$
です。他方、先に見たように、\(\|\mathbf{c}(t)\| = 1\) より、\(\mathbf{c}(t)\) は単位球面上の曲線でもあります。
これより、\(\mathbf{c}(t)\) が単位球面と \(\mathbf{p}\) と \(\mathbf{a}\) が生成する平面の交線であることが分かりました。以下では、具体的な数値例などを用いてこのことを確認していきます。
平面の法線ベクトル
\( \mathbf{p},\; \mathbf{a} \) を以下の通り定めます。(図2)
$$
\mathbf{p} = \frac{1}{\sqrt{3}}\begin{pmatrix} 1\\ -1\\ 1 \end{pmatrix}, \:\:\: \mathbf{a} = \frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2\\ 1 \end{pmatrix}
$$
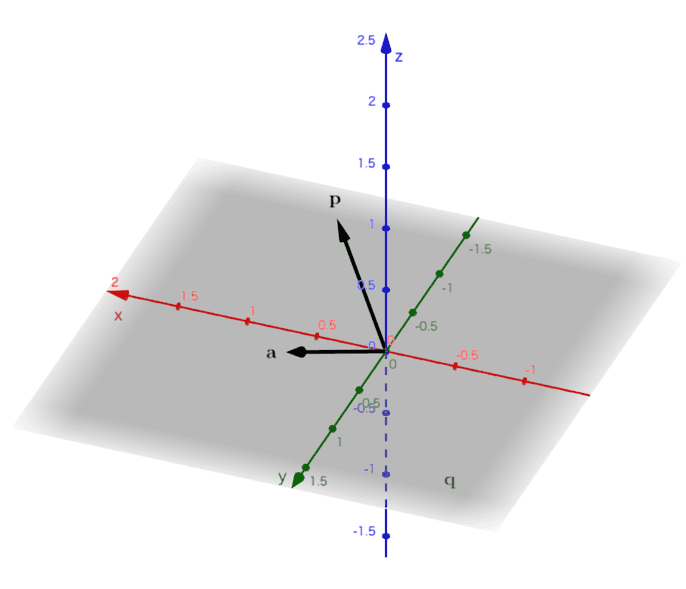 (図2) ベクトル\( \mathbf{a} \)とベクトル\( \mathbf{p} \)
(図2) ベクトル\( \mathbf{a} \)とベクトル\( \mathbf{p} \)
\(\mathbf{p}\) と \(\mathbf{a}\) は、互いに直交していて、いずれのノルムも 1 になっています。このとき、\(\mathbf{p}\) と \(\mathbf{a}\) が張る平面を \(T\) とすると
$$
\begin{align*}
T &= \mathrm{Span}[\mathbf{p}, \mathbf{a}]\\
&=\{c_1 \mathbf{p} + c_2 \mathbf{a}\;|\; c_i \in \mathbb{R}\}
\end{align*}
$$
ですが、この表し方だと後で不便になるので、法線ベクトルを用いた表現方法で表し直します。
そこで、まず平面 \(T\) の法線ベクトルを \(\mathbf{u} = (u_1, u_2, u_3)^\top\) とおきます。平面の方程式は、法線ベクトルに直交するすべてのベクトル(点)の集合として表すことができます。
今回の場合、平面 \(T = \mathrm{Span}[\mathbf{p}, \mathbf{a}]\) 上のすべてのベクトルと \(\mathbf{u}\) が直交しなければなりません。
これを満たすためには、平面 \(T\) を生成する基底ベクトル \(\mathbf{p}\) と \(\mathbf{a}\) の両方が法線ベクトル \(\mathbf{u}\) と直交していることが必要十分条件です。従って、
$$
\begin{cases}
\mathbf{p} \cdot \mathbf{u} = 0 \\
\mathbf{a} \cdot \mathbf{u} = 0
\end{cases}
\leftrightarrow
\begin{cases}
u_1 – u_2 + u_3 = 0\\
u_1 + 2u_2 + u_3 = 0
\end{cases}
$$
という連立方程式の解が、平面 \(T\) の法線ベクトル \(\mathbf{u}\) になります。これを解けば、
$$
\begin{cases}
u_1 + u_3 = 0\\
u_2 = 0
\end{cases}
$$
を得ます。\(u_1\) と \(u_3\) は、\(u_1 + u_3 = 0\) を満たす限り任意なので、例えば \(u_1 = 1\) と \(u_3 = -1\) とします。これより、\(\mathbf{u}\) は
$$
\mathbf{u} = \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix}
$$
となります。(図3)
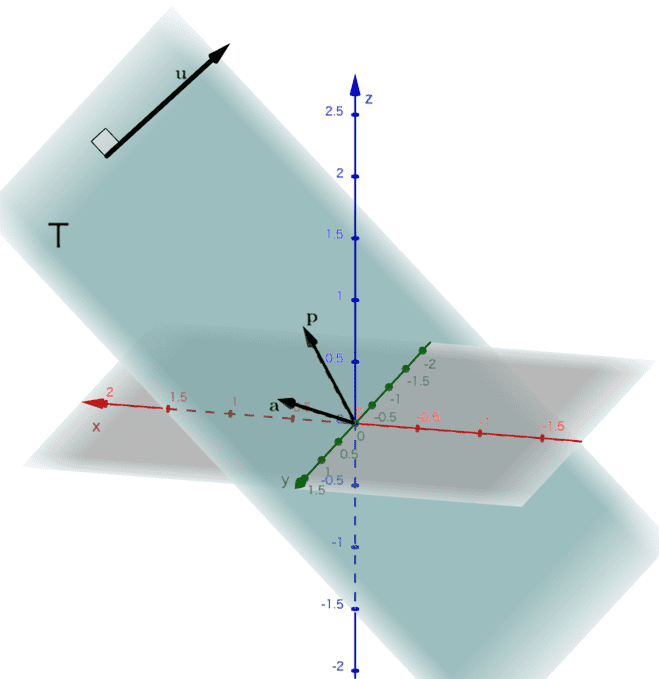 (図3) \( \mathbf{p} \)と\( \mathbf{a} \)が張る平面\( T\) と\( T\)に対する法線ベクトル\( \mathbf{u} \)
(図3) \( \mathbf{p} \)と\( \mathbf{a} \)が張る平面\( T\) と\( T\)に対する法線ベクトル\( \mathbf{u} \)
よって、\(\mathbf{p}\) と \(\mathbf{a}\) が張る平面は、\(\mathbf{u}\) と直交するすべてのベクトル \(\mathbf{x} \in \mathbb{R}^3\) の集合と言い換えることができ、
$$
T = \{\mathbf{x} \in \mathbb{R}^3 |\: \mathbf{x} \cdot \mathbf{u} = 0\}
$$
となります。すなわち、平面 \(T\) の方程式は、任意のベクトル \(\mathbf{x} = (x_1, x_2, x_3)^\top\) にとして、
$$
\mathbf{x} \cdot \mathbf{u} = 0 \leftrightarrow x_1 + 0x_2 -x_3 = 0
$$
となります。
平面と単位球面の交線
これで準備が整ったので、\(\mathbf{c}(t)\) が、単位球面と \(\mathbf{p}, \mathbf{a}\) が張る平面 \(T\) の交線になっていることを見ていきます。
まず、\(\mathbf{c}(t)\) は、
$$
\begin{align*}
\mathbf{c}(t) &= \cos(t) \mathbf{p} + \sin(t) \mathbf{a} \\\\
&= \frac{\cos(t)}{\sqrt{3}}\begin{pmatrix} 1\\ -1\\ 1 \end{pmatrix} + \frac{\sin(t)}{\sqrt{6}}\begin{pmatrix} 1\\ 2\\ 1 \end{pmatrix}
\end{align*}
$$
です。このとき、曲線 \(\mathbf{c}(t)\) 上の任意の点 \(\mathbf{x} = (x_1, x_2, x_3)^\top\) の各成分は、
$$
\begin{cases}
x_1 = \frac{\cos(t)}{\sqrt{3}} + \frac{\sin(t)}{\sqrt{6}}\\
x_2 = \frac{-\cos(t)}{\sqrt{3}} + \frac{2\sin(t)}{\sqrt{6}}\\
x_3 = \frac{\cos(t)}{\sqrt{3}} + \frac{\sin(t)}{\sqrt{6}}
\end{cases}
$$
という関係式によって規定され、これらの成分の間には、
$$
\begin{cases}
x_1 = x_3 \\
x_{1}^2 + x_{2}^2 + x_{3}^2 = 1
\end{cases}
\Leftrightarrow
\begin{cases}
x_1 + 0x_2 -x_3 = 0\\
x_{1}^2 + x_{2}^2 + x_{3}^2 = 1
\end{cases}
$$
という関係式が成立しています。すなわち、曲線 \(\mathbf{c}(t)\) は、この連立方程式の解集合です。ここで、
\[
x_1 + 0x_2 – x_3 = 0
\]
は、\(\mathbf{p}\) と \(\mathbf{a}\) が張る平面 \(T\) の方程式であり、
\[
x_1^2 + x_2^2 + x_3^2 = 1
\]
は半径1の単位球面の方程式です。
これより、\(\mathbf{c}(t)\) は単位球面上にあると同時に、\(\mathbf{p}\) と \(\mathbf{a}\) が張る平面 \(T\) 上にもあります。したがって、\(\mathbf{c}(t)\) は単位球面と平面 \(T\) の交線であることが確かめられました。(図4)
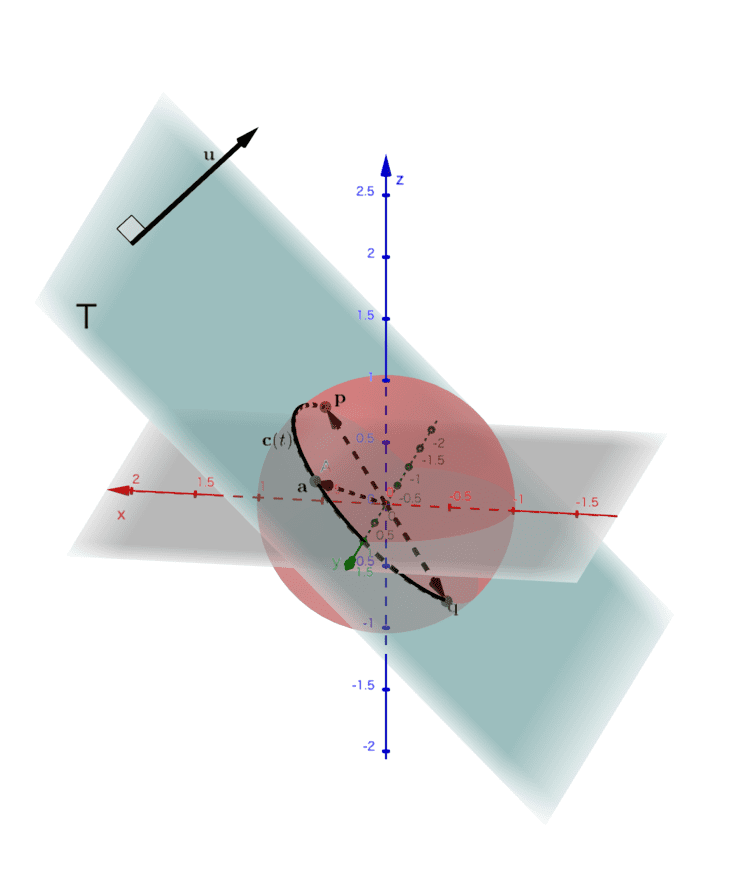 (図4) \( \mathbf{c}(t) \) は、単位球面と平面\( T\)の交線になっている
(図4) \( \mathbf{c}(t) \) は、単位球面と平面\( T\)の交線になっている
なお、この連立方程式をさらに同値変形すれば、
$$
\begin{cases}
x_1 + 0x_2 -x_3 = 0 \\
2x_{1}^2 + x_{2}^2 + 0x_{3} = 1
\end{cases}
$$
となります。\(2x_{1}^2 + x_{2}^2 + 0x_{3}^2 = 1\) は、長軸が \(1\)、短軸が \(1/\sqrt{2}\) の楕円が \(z\) 軸に沿って上下に伸びる煙突のような図形の方程式です。(図5)
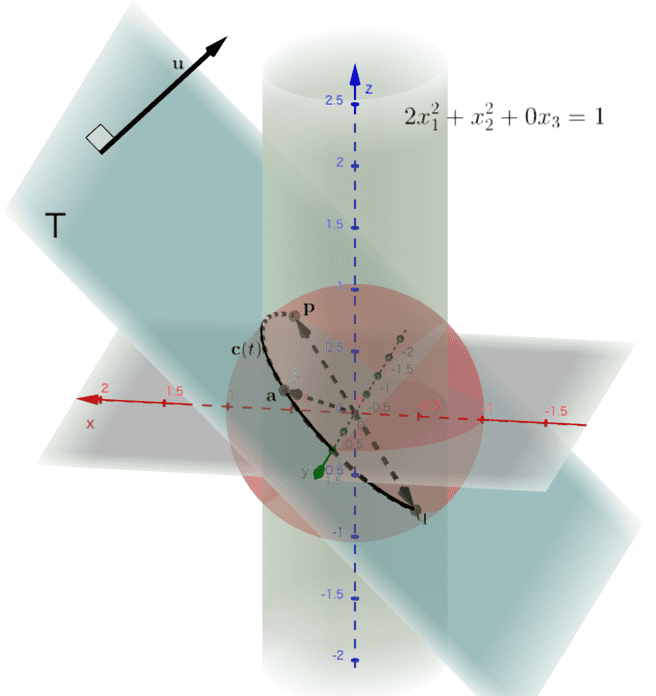 (図5) 単位球面と平面\( T\)の交線\( \mathbf{c}(t) \) を大局的に見ると、楕円型の煙突のような図形の側面の一部であることがわかる。
(図5) 単位球面と平面\( T\)の交線\( \mathbf{c}(t) \) を大局的に見ると、楕円型の煙突のような図形の側面の一部であることがわかる。こちらのリンクから、記事内の画像で使ったGeoGebra のページに遷移できます。
参考文献
本記事は、【ラング 続解析入門】をもとに作成しました。「多変数微積分やベクトル解析を勉強したいけど、いい教科書・参考書に出会えていない」という方には、特にオススメできる1冊です。


