この記事では、十分条件と必要条件を基礎から丁寧に解説します。
まず、十分条件と必要条件を理解するための基礎・前提となる命題・述語・真理集合から始めます。
その後、本題の十分条件と必要条件に関して、イメージ図も用いて詳細に説明します。
この記事を読めば、十分条件と必要条件とはなんなのか?また、それぞれがどのように役立つのかが分かるはずです。
命題・述語・真理集合
ここでは、十分条件・必要条件を理解するための基礎となる「命題・述語・真理集合」について手短に解説します。
命題
命題とは、真または偽(正しいor正しくない)を明確に判別できる文や式のことをいいます。
例えば、\(2>1 \) は「真」命題です。一方、\(1+1 = 0 \) は「偽」の命題です。
述語(条件)
述語とは、文字を含んでいて、それ単体では真or偽を判定できない文や式です。述語のことを条件ともいいます。いずれにしても、述語(条件)とは、「変数を含んでいるために命題になりきっていない文や式」だといえます。
例えば、\( x > 1\)は述語です。\( x\)の値が変数で具体的に定まっていないので 、真偽の判定ができないからです。ここで\( x=2\) を代入すると\( 2>1\)となり真の命題になります。他方、\( x=0\) を代入すると\(0 >1 \)で偽の命題になります。
述語に含まれる文字は、自由変数と言い、自由変数の取り得る範囲(自然数なのか実数なのかなど)を変域(または普遍集合)といいます。
先の例\( x > 1\) では、\( x\) が自由変数で、変域に関しては特に指定はしませんでした。もちろん本来は、自由変数の変域は重要です。ただ、本記事では深入りしないことにします。
このように、述語は、その自由変数に値を代入することで命題になります。また一般的に、述語は\( P(x)\) という形で表され、これを「自由変数\( x\) に関する述語」と呼びます。
真理集合
述語とは、文字を含んでいて、命題になりきっていない文や式のことでした。そして、述語の自由変数に何らか具体的な値を代入することで、真の命題or偽の命題のいずれかになるのでした。
ここで、述語\( P(x)\)に対して、命題\( P(a)\) が真になる全ての\( a\) を集めてできる集合という考えが、割と自然に出てくるのは納得できるのではないでしょうか。
ざっくりとした説明ですが、これが述語に対する真理集合という概念です。真理集合を厳密に定義すると以下になります。
自由変数\(x\)に関する述語\(P(x)\)の真理集合とは、\(x\)の変域(普遍集合)を\(U\)としたとき、\(a\in U\)に対して、命題\(P(a)\)が真になる全ての\(a\)からなる\(U\)の部分集合\(\{x\in U|P(x)\} \subset U\)
具体例を見てみましょう。自由変数\( x\) に関する述語\(P(x)\)を\( x>5\) とします。また、\( x\) の変域を\( U\) として、\(U \)は、1以上10以下の自然数とします。
このとき、\( P(x)\) の真理集合\(\{x \in U|\; P(x)\} \) は、
\[\{x \in U|\; P(x)\} = \{6,7,8,9,10\}\]
となります。
ここまでで、十分条件と必要条件を理解するための準備が終わりました。
十分条件と必要条件
まずは、十分条件と必要条件をしっかりと定義します。
変数\(x\)の変域を\(U\)として、\(P(x),\,Q(x)\)を自由変数\(x\)に関する述語とする。このとき、
\[\{x|\;P(x)\} \subset \{x|\;Q(x)\}\]
が成り立つならば、すなわち、\(P(x)\)の真理集合が\(Q(x)\)の真理集合の部分集合であるとき、\(P(x)\)を\(Q(x)\)の十分条件、\(Q(x)\)を\(P(x)\)の必要条件という。
「論理と集合から始める数学の基礎」p28
形式的に定義しましたが、では、ある条件が別の条件の十分条件であるとき、それは何を意味するのでしょうか?
同様に、ある条件が別の条件の必要条件であるとき、それは何を意味するのでしょうか?
以降では、これら十分条件・必要条件の実質的な意味や活用法について探っていきます。
ある条件が別の条件の「十分条件」であることの意義
条件\(P(x)\)が条件\(Q(x)\)の十分条件であるとします。このとき、\(P(x)\)は、\(Q(x)\)の成立保証条件として機能します。
つまり、\(P(x)\)を成立させる\(x\)は、\(Q(x)\)も必ず成立させます。
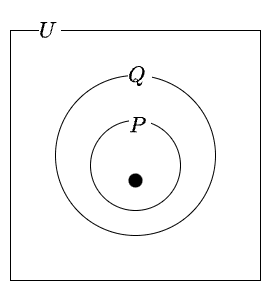 十分条件のイメージ図
十分条件のイメージ図なぜなら、\(\{x|\;P(x)\} \subset \{x|\;Q(x)\}\)より、\(P(x)\)の真理集合\(\{x|\;P(x)\}\)の要素である\(x\)は、必ず\(Q(x)\)の真理集合\(\{x|\;Q(x)\}\)の要素になるからです。
イメージ図では、黒丸が\( P(x)\) を成立させる\( x\) に相当します。明らかに、黒丸は\(Q(x) \) の真理集合にも含まれています。つまり、\( Q(x)\) も満たしています。
一方で、十分条件を運用する際には、ある\(x\)が\(P(x)\)を成立させなかったとしても、その\(x\)が、必ず\(Q(x)\)も成立させないことを意味するわけでない点には注意する必要があります。
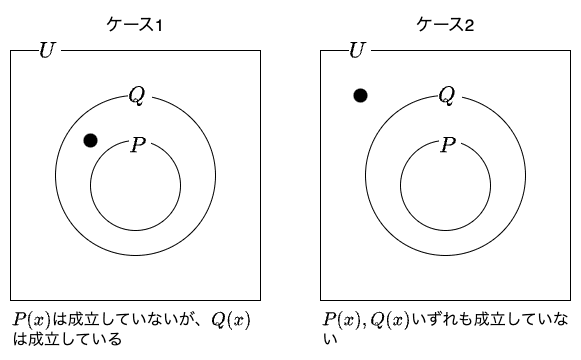 十分条件を運用する際の注意点
十分条件を運用する際の注意点つまり、ある\(U\)の要素\(x\)が\(Q(x)\)の十分条件\(P(x)\)を満たさなかったとしても、この事実だけでは、その\(x\)が\(Q(x)\)を満たすか否かについては、不明であり何も言えないということです。
ある条件が別の条件の「必要条件」であることの意義
条件\(Q(x)\)が条件\(P(x)\)の必要条件であるとします。このとき、\(Q(x)\)は、\(P(x)\)を成立させうる候補絞込み条件として機能します。
つまり、必要条件\(Q(x)\)すら満たさない\(x\)は、\(P(x)\)を満たすことは100%あり得なく、他方、必要条件\(Q(x)\)を満たす\( x\)は、\( P(x)\) を満たす可能性のある候補となります。
なぜなら、\(\{x|\;P(x)\} \subset \{x|\;Q(x)\}\)より、\(Q(x)\)の真理集合\(\{x|\;Q(x)\}\)の要素でない\(x\)は、絶対に\(P(x)\)の真理集合\(\{x|\;P(x)\}\)の要素にはなり得ないからです。
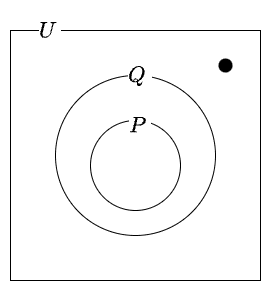 必要条件のイメージ
必要条件のイメージイメージ図では、黒丸が\( P(x)\) の必要条件\( Q(x)\) すら満たさない\( x\) に相当します。必要条件\( Q(x)\) の真理集合に入らないなら、\( P(x)\)の真理集合に入る可能性がゼロなのがみて取れます。
逆に、必要条件\( Q(x)\) の真理集合に入っていれば、\( P(x)\) を満たす可能性のある候補として扱えることも分かります。
ここで、必要条件は、あくまで候補絞込み条件でしかない、ということはしっかり理解する必要があり、必要条件を運用する際の注意点です。
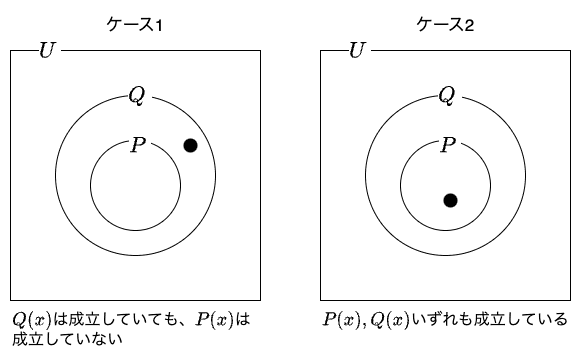 必要条件の注意点
必要条件の注意点つまり、ある\(U\)の要素\(x\)が\( P(x)\)の必要条件 \(Q(x)\)を満たしたとしても、その\(x\)が直ちに\(P(x)\)を満たすことを保証するわけではない、ということです。
ケース1では、必要条件\( Q(x)\)は満たしているけれども、\( P(x)\) は満たしていない例です。
ケース2では、必要条件\( Q(x)\) を満たし、かつ、\( P(x)\)も満たしている例です。
ケース1,2のどちらかは、\( x\) が\( P(x)\) の必要条件\( Q(x)\) を満たしているという事実だけからは判定できません。だからこそ、必要条件は、候補絞り込み条件なのです。
必要十分条件
ここまでで、十分条件と必要条件をみてきましたが、これら2つが同時に成立することとして、必要十分条件という概念が定義されます。
まずは、必要十分条件の定義を確認しておきます。
\(P(x)\)が\(Q(x)\)の十分条件でもあり、かつ、必要条件でもあるとき、\(P(x)\)は\(Q(x)\)の必要十分条件であるという。
「論理と集合から始める数学の基礎」p29
ここで、\(P(x)\)が\(Q(x)\)の必要十分条件であるとき、\(Q(x)\)が\(P(x)\)の必要十分条件になっていることにも注意しましょう。
以降では、全ての説明で、主語を\( P(x)\)にして行いますが、\(Q(x)\)を主語にしても同様に成り立ちます。
必要十分条件が成り立つときの真理集合の関係性
\( P(x)\) が\(Q(x)\)の必要十分条件であるとき、\(P(x),\,Q(x)\)の真理集合はどのような関係になるのかみていきます。
まず、\(P(x)\)は\(Q(x)\)の十分条件だから、定義より
\[\{x|\;P(x)\} \subset \{x|\;Q(x)\}\]
同時に、\(P(x)\)は\(Q(x)\)の必要条件でもあるから、定義より
\[\{x|\;Q(x)\} \subset \{x|\;P(x)\}\]
つまり、\( P(x)\) が\(Q(x)\)の必要十分条件であるとき、
\[\{x|\;P(x)\} \subset \{x|\;Q(x)\} \mathrm{かつ} \{x|\;Q(x)\} \subset \{x|\;P(x)\}\]
が成り立っています。ここから、\(P(x)\)の真理集合と\(Q(x)\)の真理集合は、集合の相当の定義から、
\[\{x|\;P(x)\} = \{x|\;Q(x)\}\]
すなわち、\(P(x)\)が\(Q(x)\)の必要十分条件であるとは、これら2つの述語の真理集合は一致する(等しい)ことを意味わけです。
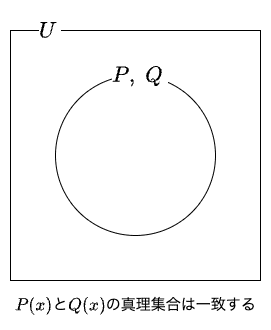 必要十分条件のイメージ図
必要十分条件のイメージ図さらに、このとき、\(P(x)\)と\(Q(x) \) は同値であるともいい、それは
\[P(x) \Leftrightarrow Q(x)\]
と表されます。
【「集合の相当」に関する補足】
一般に、2つの集合\(A,B \) において、
\[A \subset B \mathrm{かつ} B \subset A\]
が成り立つとき、集合\( A\)と\(B\)は等しいと定義され、 \( A=B\)で表します。また、これを集合の相当と言います。
「論理と集合から始める数学の基礎」p3, 45
ある条件が別の条件の必要十分条件であることの意義
\(P(x)\)が\(Q(x)\)の必要十分条件であるとします。このとき、\(P(x)\)が成立するなら、必ず\(Q(x)\)も成立し(青丸)、また、\(P(x)\)が成立しないなら、必ず\(Q(x)\)も成立しません(赤丸)。
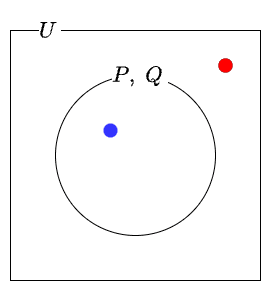 必要十分条件のイメージ図2
必要十分条件のイメージ図2なぜなら、\( \{x|\;P(x)\} = \{x|\;Q(x)\}\) より、\( P(x)\) の真理集合\(\{x|\;P(x)\} \) の要素である\( x\) は、必ず\( Q(x)\) の真理集合の要素になり、他方、\( P(x)\) の真理集合\(\{x|\;P(x)\} \) でない\( x\) は、必ず\( Q(x)\) の真理集合の要素 にならないからです。
つまり、\(P(x)\)が\(Q(x)\)の必要十分条件であるとき、\(P(x)\)は\(Q(x)\)の成立保証条件、候補絞り込み条件、両方の機能を持つわけです。
【補足】「ならば\(\rightarrow \)」と十分条件・必要条件の関係性
大学数学を勉強していると、\( P \mathrm{ならば} Q\) という形式の定理が頻出することに気づきます。
例えば、「\(f(x)\)が\( x=c\) で極値をとるならば\( f'(c)=0\)」だったり、「級数 \( \sum|a_n|\) が収束するならば、級数\( \sum a_n\) も収束する」です。
そして、このとき、\( P\) は\(Q\)の十分条件であるといい、\(Q\)は\(P\)の必要条件であるといいます。
ここで、ここまでの十分条件と必要条件の議論と\( P \mathrm{ならば} Q\)における十分条件と必要条件の関係性について、いまいちパッとしないと感じる方は少なくないのではないでしょうか?
少なくとも自分は、大学数学を学び始めた頃、全く釈然としませんでした。というより、完全に混同してしまっていました。
本記事では、\( P \mathrm{ならば} Q\)における十分条件と必要条件の関係性について詳細に解説することはしません。なぜなら、前提となる予備知識がたくさんあり、とてもこの記事内では収まらないからです。
この関係性をしっかり理解するには、「論理と集合から始める数学の基礎」第1章〜第3章を読んでみてください。
ただし、ここで一つだけ補足するなら、論理演算子\(\rightarrow \) (ならば)と十分条件・必要条件は、それぞれが独立した概念だということです。
参考図書
本記事を執筆するにあたり、「論理と集合から始める数学の基礎」を参考にさせて頂きました。
大学数学をより深く本質的に理解するために必要なことが凝縮されていて、本当に素晴らしい書籍です。
大学数学を学んでいる人、または、理系の大学1,2年生が、微積分や線形代数と同時並行で使っていくのがよいと思います。



