本記事では、「直線のパラメータ(媒介変数)表示」を解説していきます。記事の構成は以下の通りです。
最初のセクションは、直線のパラメータ表示を直観的に理解できるように、沢山の図を用いながらイメージ重視の解説をしています。また、「直線の方程式」との関連にも触れています。
直線のパラメータ表示があまり理解できていない人でも、この最初のセクションを読むだけで、直線のパラメータ表示に関する理解度・解像度は劇的に改善されるはずです。
ここまでが基礎編です。
次のセクションでは、論理と集合を用いて、直線のパラメータ表示を厳密に導出・定義していきます。
数学が好きな人は、是非この部分まで読んで、直線のパラメータ表示の「真の姿・正体」を理解してください。
最後に、直線のパラメータ表示と密接に関連するより高度な諸概念として、1次元線形部分空間と凸結合を取り上げます。
このように、本記事は、直線のパラメータ表示を直感的かつざっくりと理解したい初心者から、これの厳密な導出や定義を知りたい中級者まで、幅広い読者の方のニーズを満たせるように執筆してあります。
直線のパラメータ表示とは? 〜直感的な理解を目指して〜
この最初のセクションでは、図を用いつつ、1からstep by stepで直線のパラメータ表示を構成していくことを通じて、直線のパラメータ表示に対する直感的な理解を身につけていきます。
まず、直線のパラメータ表示とは、ざっくり言えば、
- 直線の方向
- 直線が通る1点
という2要素と媒介変数(パラメータ)を用いて、幾何的な直線を表現する手法です。以下では直線のパラメータ表示を
- 直線の方向
- 直線が通る2点
のどちらにフォーカスするかに基づき2パターンに分類して個別に解説していきます。その後、「直線の方程式」を解説します。
「直線の方向」にフォーカスした直線のパラメータ表示
ここでは、「点\(\mathbf{p}=(-2,3,1)\)を通り、ベクトル\(\mathbf{a}=(3,3,2)\)の方向をもつ直線」のパラメータ表示
\[\mathbf{x} = \mathbf{p} + t\mathbf{a} \;\;\; (t \in \mathbb{R})\]
を考えます。このパラメータ表示を1から構成していくことを通じて、直線のパラメータ表示とこれが表す直線をヴィジュアルかつ直感的に理解できることを目指します。
ではまずは、「直線の方向」を決めます。直線のパラメータ表示では、直線の方向は、1つの(矢印としての幾何)ベクトルで定めます。
この直線の方向を決定するベクトルを「(直線の)方向ベクトル」と言います。ここでは、方向ベクトルとして\(\mathbf{a}=(3,3,2)\)を取ります(図_1-1)。
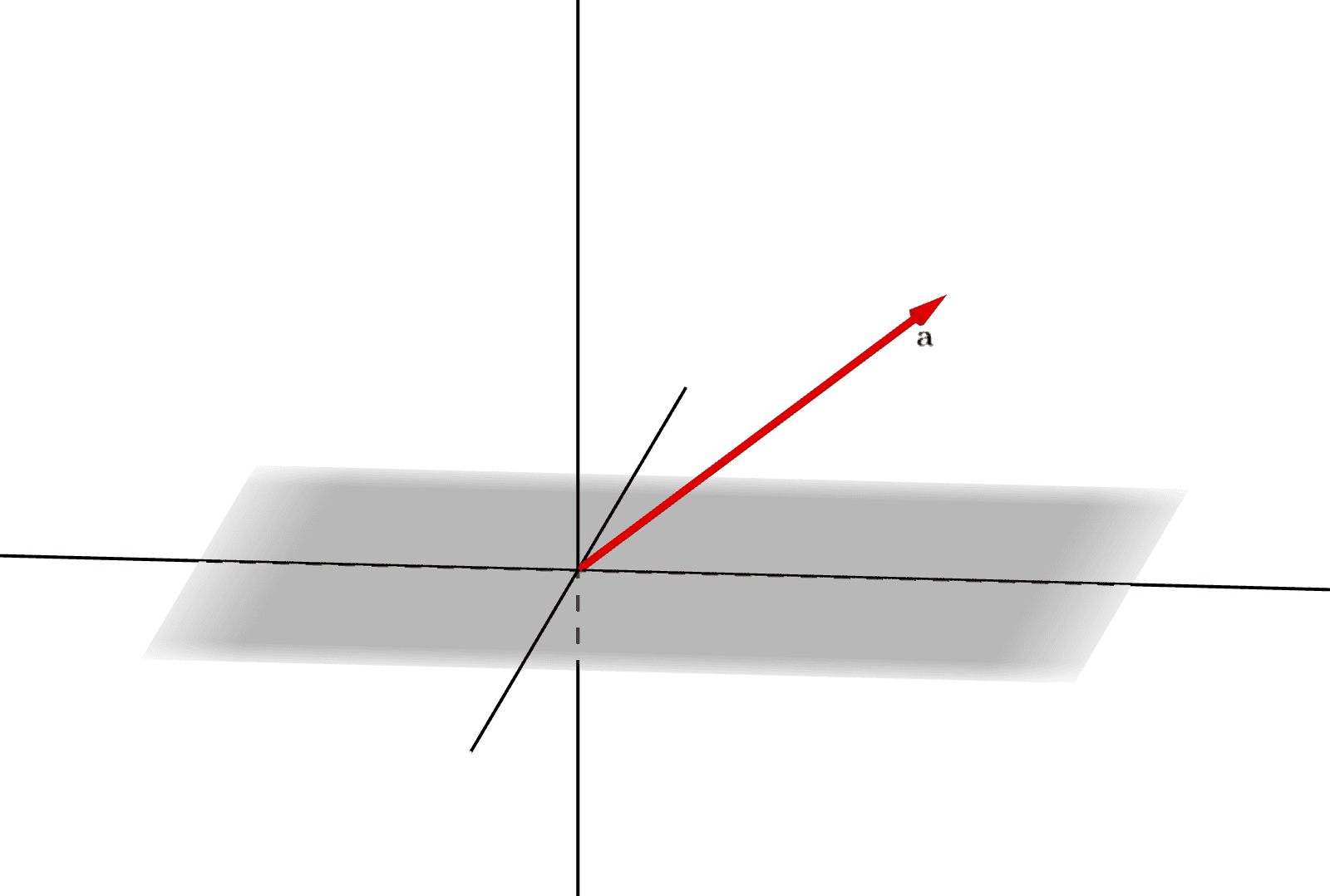 図_1-1
図_1-1
直線の方向が定まりました。次は、\(\mathbf{a}\)に対して、実数\(\mathbb{R}\)を変域とするスカラー変数\(t\)をかけます。つまり、\(t\mathbf{a}\)です。そして、\(t\)を\(\mathbb{R}\)上で任意に動かします。このことを数式でラフに表現すると、
\[t\mathbf{a}\;\;\; (t \in \mathbb{R})\]
です。すると、図のように、原点\(\mathbf{0}\)を通り、ベクトル\(\mathbf{a}\)の方向をもつ直線が描画できました(図_1-2)。
 図_1-2
図_1-2
ここで、\(t\)は\(\mathbb{R}\)上を連続的に任意に動いていますが、ある特定の\(t_i\)や\(t_j\)に着目したとき、\(t_i\mathbf{a}\)や\(t_j\mathbf{a}\)は、直線\(t\mathbf{a}\)上の1つの点であることに注意しましょう(図_1-3)。
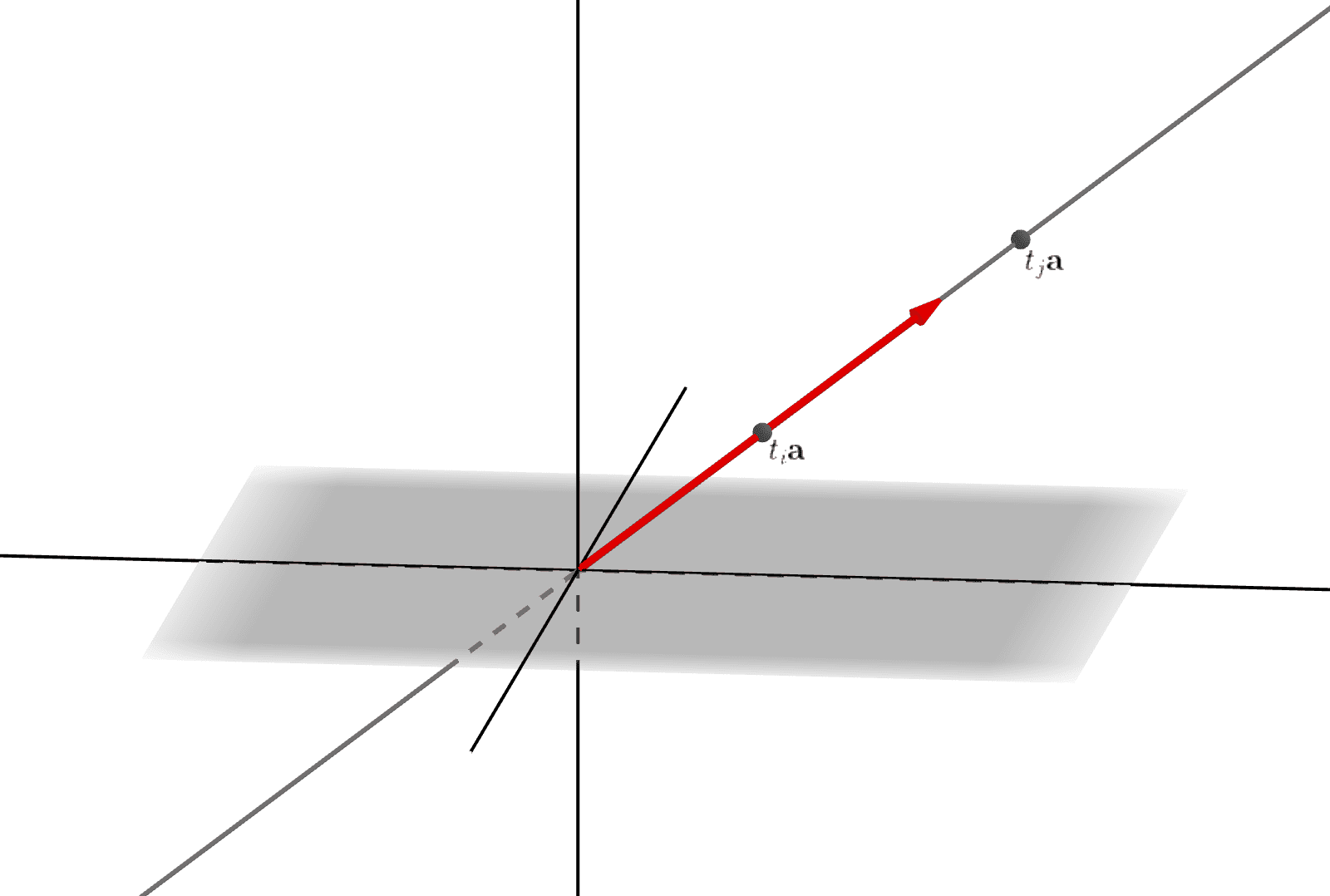 図_1-3
図_1-3
さて、直線\(t\mathbf{a}\;\;\; (t \in \mathbb{R})\)は、原点\(\mathbf{0}\)を通りますが、原点以外を通したいこともあります。ここでは、点\(\mathbf{p} = (-2, -3, 1)\)を取り、直線が点\(\mathbf{p}\)を通るようにします(図_1-4)。
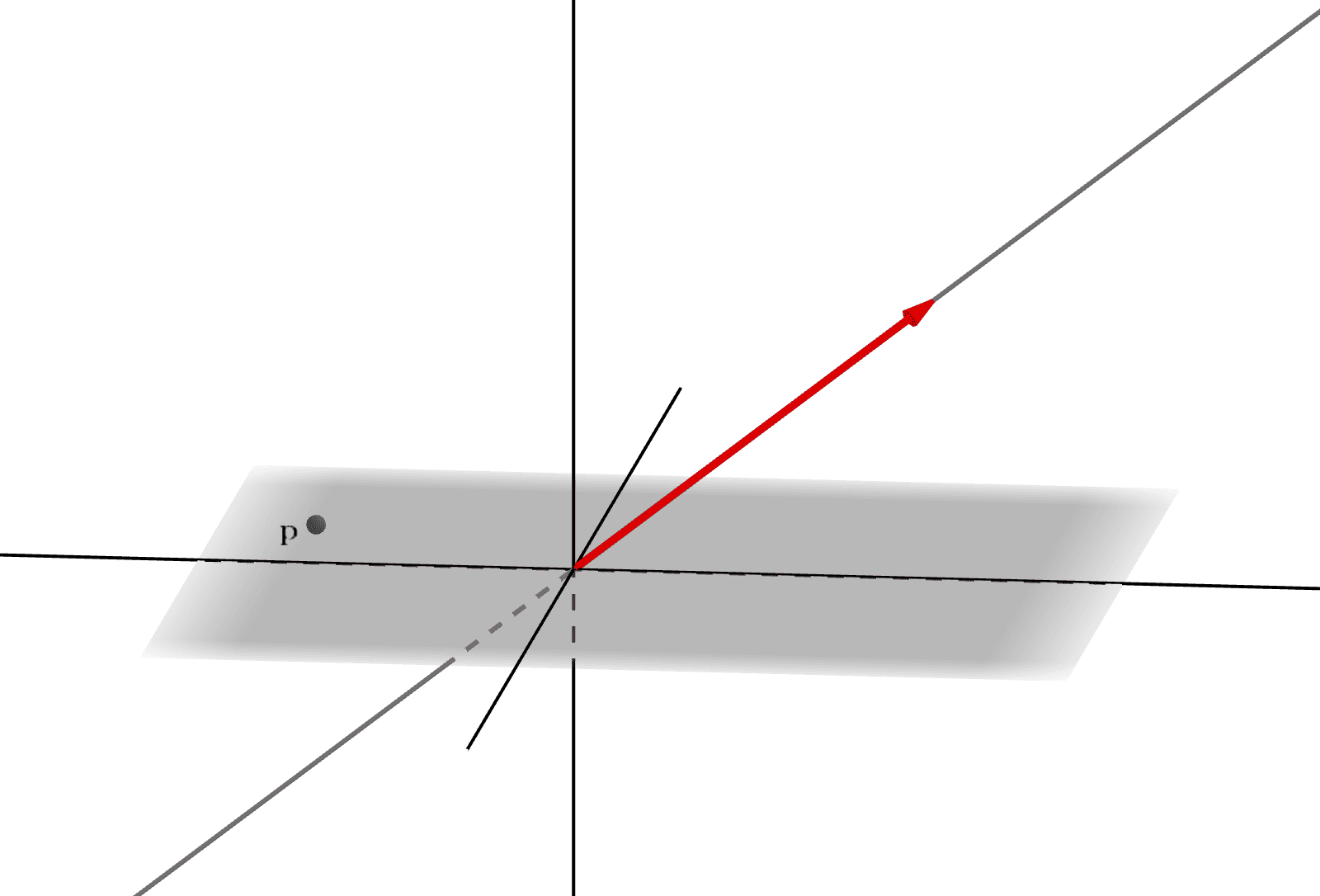 図_1-4
図_1-4
そのためには、\(\mathbf{p}\)を通るように、直線\(t\mathbf{a}\;\;\; (t \in \mathbb{R})\)を(向きは同じのまま)平行移動させる必要があります。すなわち、直線上の無数の点
\[t_1\mathbf{a},\; t_2\mathbf{a},\; \ldots, t_n\mathbf{a},\; \ldots\]
全てに対して、\(\mathbf{p}\)との和
\[\mathbf{p}+t_1\mathbf{a},\; \mathbf{p}+t_2\mathbf{a},\; \ldots, \mathbf{p}+t_n\mathbf{a},\; \ldots\]
を取ります。
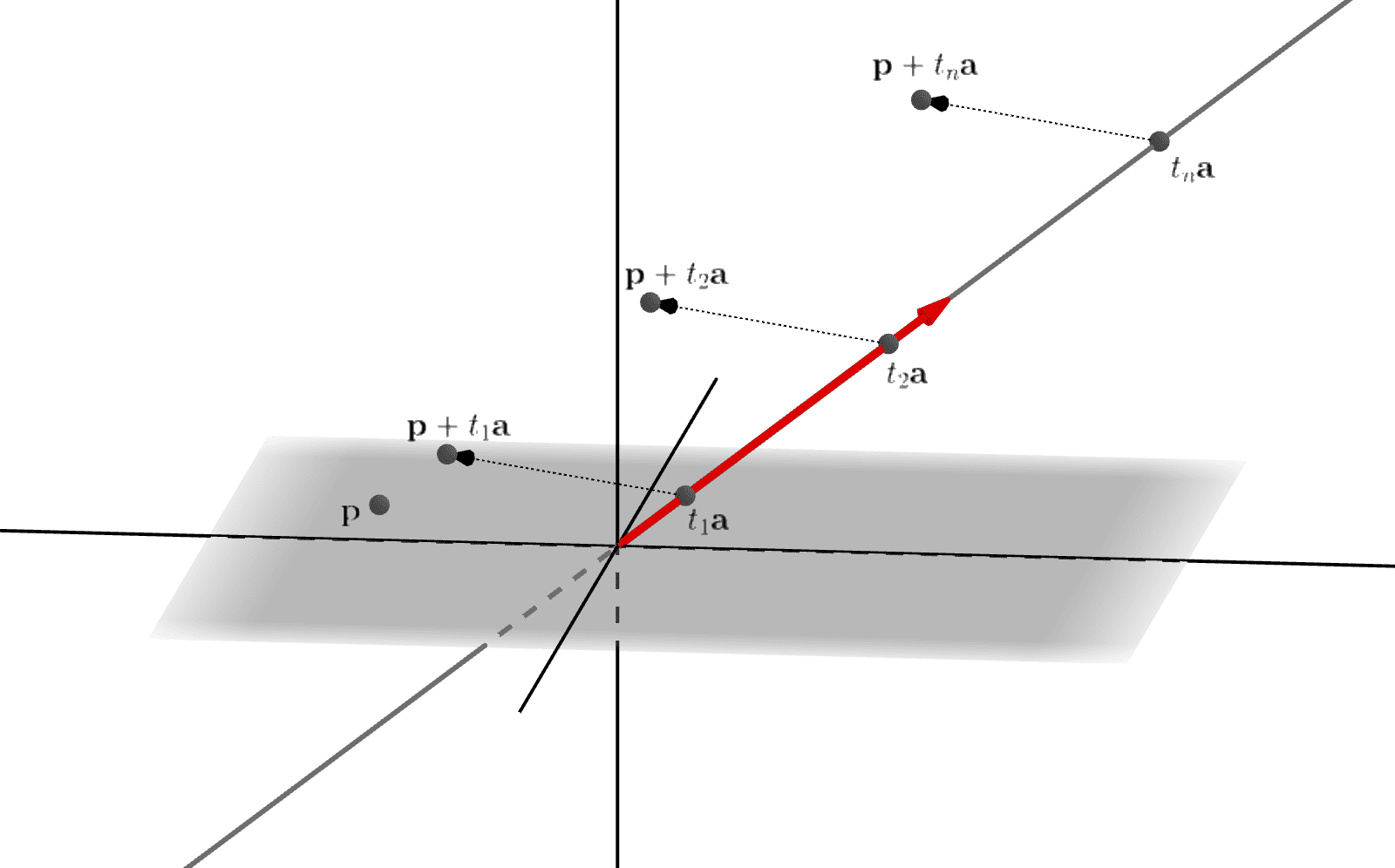 図_1-5
図_1-5
上の図_1-5では、たった3つの点の平行移動しか表現することができませんが、実際は、無数の全ての点が平行移動しています。
そして、無数の点が集まった結果として直線が出来上がるので、平行移動後の(無数の)点を全て集めると、それは点\(\mathbf{p}\)を通り、\(\mathbf{a}\)の方向をもつ直線そのものです(図_1-6)。
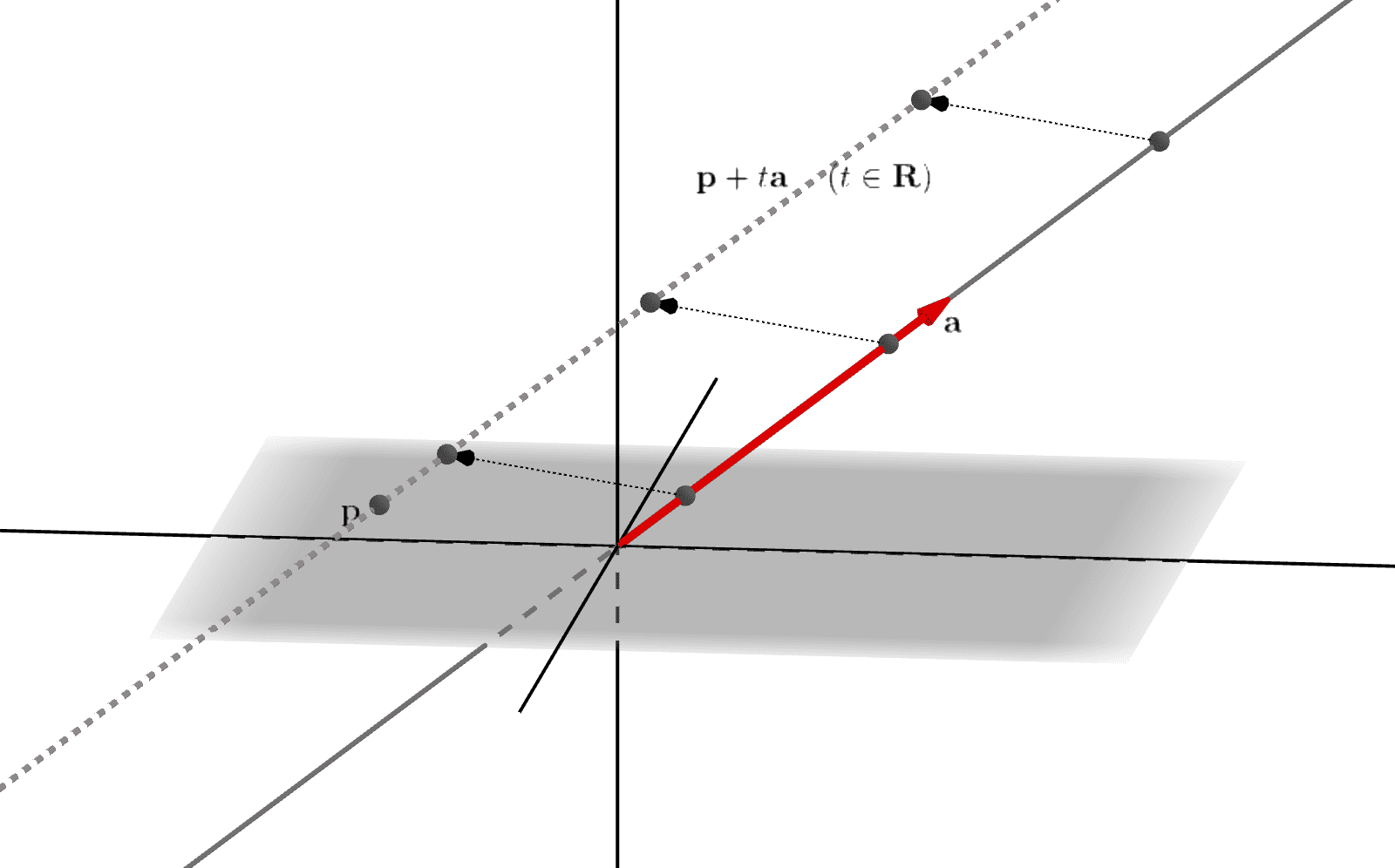 図_1-6
図_1-6
また、この一連の平行移動をより簡潔に表せば、
\[\mathbf{p} + t\mathbf{a} \;\;\; (t \in \mathbb{R})\]
であり、後は、\(\mathbf{x}=\)という等式の形で表せば、
\[\mathbf{x} = \mathbf{p} + t\mathbf{a} \;\;\; (t \in \mathbb{R})\]
点\(\mathbf{p}\)を通り、\(\mathbf{a}\)の方向をもつ直線のパラメータ方程式を構成でき、このような直線を\(\mathbb{R}^3\)に描画することができました。
この直線は、特に\(t=0\)で点\(\mathbf{p}\)を、\(t=1\)で点\(\mathbf{p}+\mathbf{a}\)をそれぞれ通ります。
「直線が通る2点」にフォーカスした直線のパラメータ表示
直前では、直線が通る1点\(\mathbf{p}\)と直線の方向ベクトル\(\mathbf{a}\)を用いた直線のパラメータ表示
\[\mathbf{x} = \mathbf{p} + t\mathbf{a} \;\;\; (t \in \mathbb{R})\]
によって、3次元空間(\(\mathbb{R}^3\))に直線を描画しました。このパラメータ表示は、直線の方向を方向ベクトル\(\mathbf{a}\)を用いて直接的に指定するという意味で、「直線の方向」にフォーカスした直線のパラメータ表示と言えそうです。
この形式のパラメータ表示で表される直線は、2点\(\mathbf{p}\)と\(\mathbf{p} + \mathbf{a}\)を通りますが、後者は、通る1点\(\mathbf{p}\)と方向ベクトル\(\mathbf{a}\)の和としての点です。
ここから分かるのは、「直線の方向」にフォーカスした直線のパラメータ表示では、直線が通る2点を柔軟に決めづらいということです。つまり、通る1点\(\mathbf{p}\)は自由に決めれますが、もう1つの点は、方向ベクトル\(\mathbf{a}\)によって自動的に\(\mathbf{p}+\mathbf{a}\)と決まってしまいます。
そこで、直線のパラメータ表示の別の方法として、「直線が通る2点」にフォーカスした形式を考えてみたいと思います。
ここでは、2点\(\mathbf{p},\mathbf{q}\)を通る直線を、直線のパラメータ表示によって表していきます(図_1-7)。
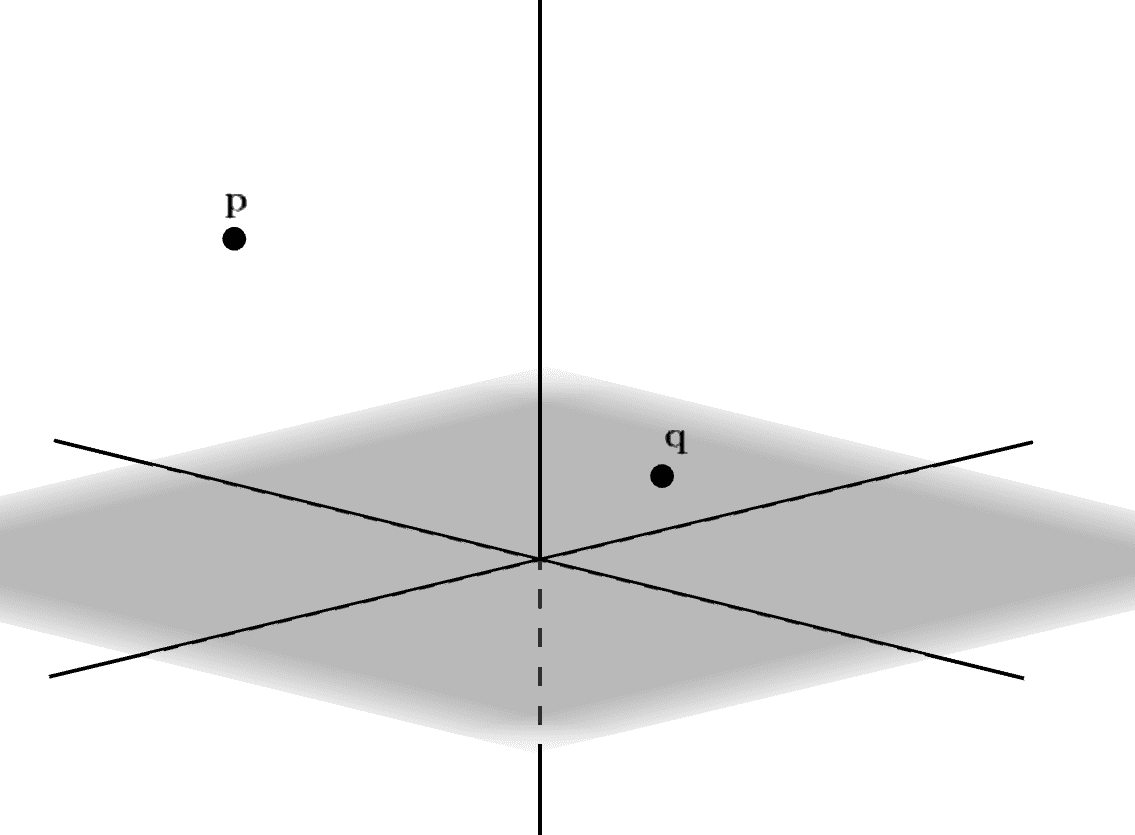 図_1-7
図_1-7
まず前提として、「直線の方向」、「直線が通る2点」、いずれにフォーカスするとしても、冒頭でも言った通り、直線のパラメーター表示は
- 直線の方向
- 直線が通る1点
という2要素で構成されるということです。従って、ここでの「直線が通る2点」にフォーカスする場合、直線の方向の表し方が重要になります。
そこで、直線が2点\(\mathbf{p},\mathbf{q}\)を通る、ということを考えてみます。すると、それは、この直線が、点\(\mathbf{p}\)から点\(\mathbf{q}\)に向かう方向を有している、ということです。
そして、この方向は、始点が\(\mathbf{p}\)、終点が\(\mathbf{q}\)のベクトル、つまり、ベクトル\(\mathbf{q}-\mathbf{p}\)で表せます(図_1-8)。
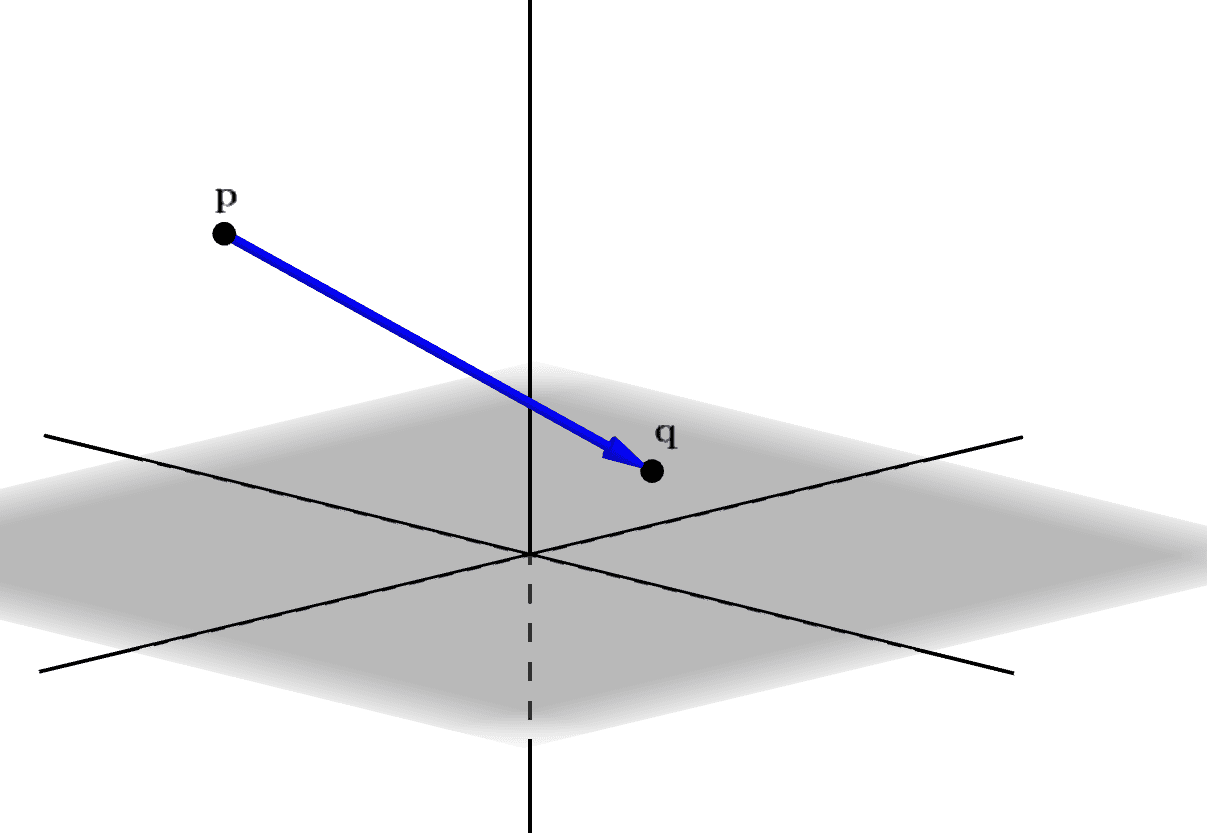 図_1-8
図_1-8
ただし、ベクトル\(\mathbf{q}-\mathbf{p}\)は、始点が原点\(\mathbf{0}\)、終点が\(\mathbf{q}-\mathbf{p}\)というベクトルでもある点に注意しましょう(図_1-9)。
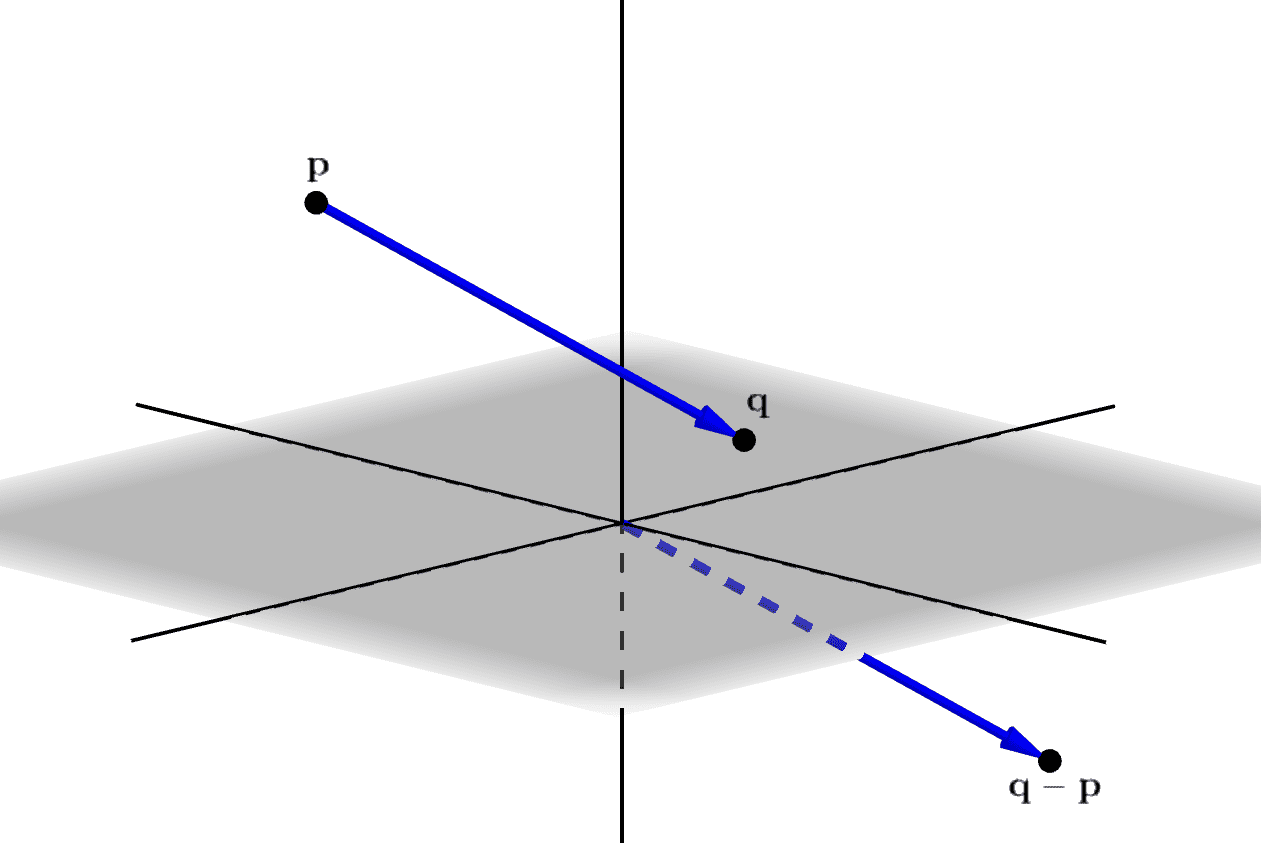 図_1-9
図_1-9
このような見方は基本的ですが、『空間における「ベクトル」という概念とその本質: 空間の点、順序対、有向線分の統一的な理解』で重点的に解説しているので必要なら参考にしてください。
さて、ここまで出来れば、後は先ほどと全く同様。このベクトル\(\mathbf{q}-\mathbf{p}\)に実数\(\mathbb{R}\)を変域とする変数\(t\)をかけて\(t\)を\(\mathbb{R}\)上を任意に動かす、つまり
\[t (\mathbf{q}-\mathbf{p})\;\;\; (t \in \mathbb{R})\]
は、原点\(\mathbf{0}\)を通り、方向ベクトル\(\mathbf{q}-\mathbf{p}\)を持つ直線です(図_1-10)。
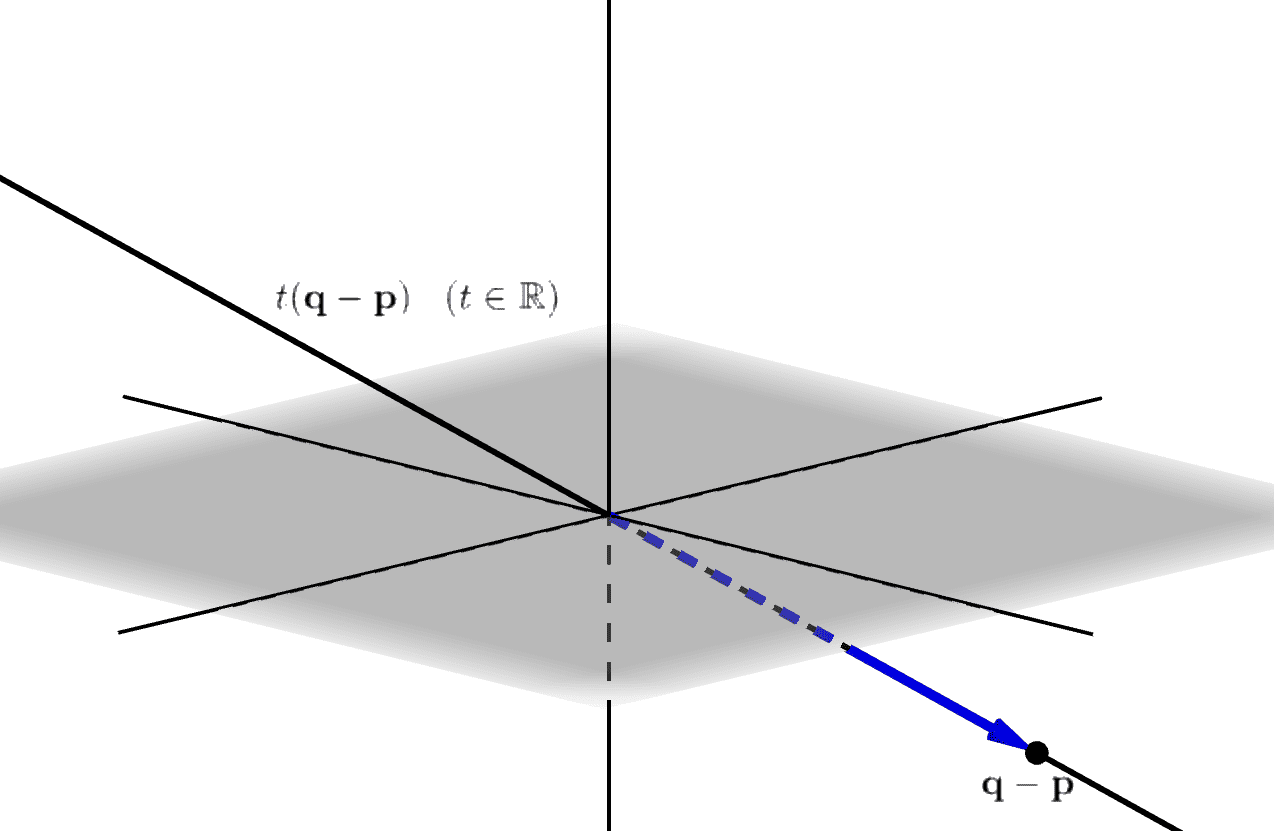 図_1-10
図_1-10あとはこの直線を\(\mathbf{p}\)(または\(\mathbf{q}\))だけ平行移動させることで、2点\(\mathbf{p},\mathbf{q}\)を通る直線
\[\mathbf{x} = \mathbf{p} + t (\mathbf{q}-\mathbf{p})\;\;\; (t \in \mathbb{R})\]
のパラメーター表示が得られます(図_1-11)。
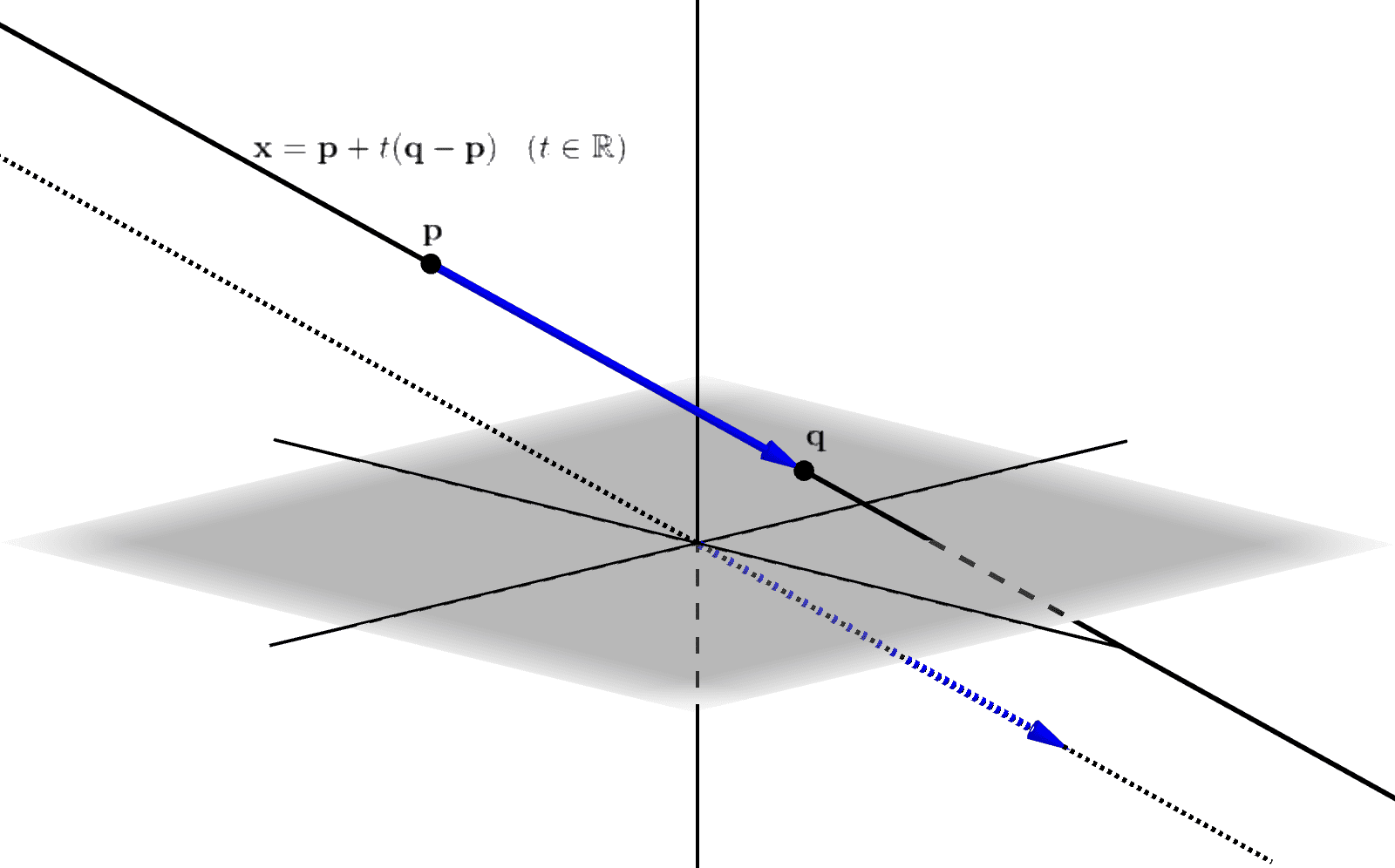 図_1-11
図_1-11
この直線は\(t=0\)で点\(\mathbf{p}\)を、\(t=1\)で点\(\mathbf{q}\)をそれぞれ通ります。
このように、「直線が通る2点」にフォーカスした直線のパラメーター表示の場合、方向ベクトルは通る2点を用いて間接的に表現されることが分かります。以下の表では、2つの直線のパラメータ表示の特徴をまとめています。

直線の方程式
直線は、パラメーター表示だけでなく、方程式(の解集合)としても表せます。まず、直線のパラメータ表示
\[\mathbf{x} = \mathbf{p}+t\mathbf{a}\;\;\; (t \in \mathbb{R})\]
を各ベクトルの成分表示として表します。ベクトルのデフォルト表記を列ベクトルとすれば、
\[\begin{pmatrix}
x_1 \\ x_2 \\ x_3
\end{pmatrix} = \begin{pmatrix}
p_1 \\ p_2 \\ p_3
\end{pmatrix}+ t\begin{pmatrix}
a_1 \\ a_2 \\ a_3
\end{pmatrix}\]
であり、これは、
\[\begin{cases}
x_1 = p_1 + ta_1 \\
x_2 = p_2 + ta_2 \\
x_3 = p_3 + ta_3
\end{cases}\]
という連立方程式です。さらに、\(t\)について解いた形で表すと
\[\begin{cases}
t = (x_1 – p_1) / a_1 \\
t = (x_2 – p_2) / a_2 \\
t = (x_3 – p_3) / a_3
\end{cases}\]
となります。この連立方程式は全て\(t=\)という形で表されているので、互いに代入し合えば、
\[t = \frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\]
を得ます。これが、点\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}\)をもつ直線の「方程式」です。より正確には、この方程式を満たす\(\mathbf{x}=(x_1,x_2,x_3)^\top\)の集合
\[\left\{\mathbf{x} \;|\; \frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\right\}\]
となります。
直線のパラメータ表示の厳密な導出と定義
このセクションでは、直線のパラメータ表示における「パラメータ(媒介変数)」の意味を明確にしつつ、
- 存在量化子が付与された3変数述語
- ベクトル値関数の値域
という異なる2つの視点から「直線のパラメータ表示」を厳密に捉え直していきます。
パラメータ(媒介変数)と存在量化子が付与された3変数述語
直線のパラメータ表示
\[\mathbf{x} = \mathbf{p} + t\mathbf{a} \;\;\; (t \in \mathbb{R})\]
において、パラメータ(媒介変数)とは、この式の\(t\)のことですが、そもそもパラメータ\(t\)とは一体何なのでしょうか。
本セクションでは、パラメータ(媒介変数)の実態を明確にしつつ、理解重視でやや曖昧な形で導入された上記の直線のパラメータ表示を厳密に導き、定義していきます。
まずは、\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}\)をもつ直線の方程式を再度取り上げます。
\[\frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\]
ここで、\(\mathbf{x}=(x_1,x_2,x_3),\; \mathbf{p}=(p_1,p_2,p_3),\; \mathbf{a}=(a_1,a_2,a_3)\)です。ここで、この方程式を、3変数\(x_1,x_2,x_3\)による3項関係\(R(x_1,x_2,x_3)\)というより広いフレームで捉え直します。
\[R(x_1,x_2,x_3) := \frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\]
もちろん、この3項関係が真になる、つまり、方程式を満たす\(\mathbf{x}=(x_1,x_2,x_3)\)を座標空間\(\mathbb{R}^3\)にプロットすると、\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}\)をもつ直線が描画されます。
さて、ここからが本題です。この3項関係\(R(x_1,x_2,x_3)\)としての直線の方程式を、既存の3変数\(x_1,x_2,x_3\)に加えて、実数\(\mathbb{R}\)を変域とする第4の変数\(t\)を、存在量化子を付加して付け加えます。つまり、まず
\[t=\frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\]
として、
\[R(x_1,x_2,x_3):=\; \exists t \in \mathbb{R},\; t= \frac{x_1 – p_1}{a_1} = \frac{x_2 – p_2}{a_2} = \frac{x_3 – p_3}{a_3}\]
と表すわけです。\( t\)は存在量化子\( \exists\)が付与されている束縛変数なので、直線の方程式は、依然として3つの自由変数からなる3項関係\( R(x_1,x_2,x_3)\)です。これをベクトル表記を使って簡潔に表し直せば、
\[R(x_1,x_2,x_3):=\;\exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t\mathbf{a}\]
を得ます。あっさり導きましたが、これこそが、直線のパラメータ表示の厳密かつ正確な表現法です。
すなわち、まず、パラメータ(媒介変数)とは、3項関係\(R(x_1,x_2,x_3)\)が存在量化子\((\exists)\)を伴う方程式(述語・条件)で定められているとき、存在量化子の対象になっている(束縛)変数のことです。
そして、座標空間\(\mathbb{R}^3\)の図形が、パラメータ(媒介変数)を用いて定められた3項関係\(R(x_1,x_2,x_3)\)を満たす\(\mathbf{x}=(x_1,x_2,x_3)\)によるプロットのとき、この3項関係を定める3変数述語(方程式)を、その図形の「パラメータ(媒介変数)表示」といいます。
よって、\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}\)を通る直線のパラメータ(媒介変数)表示の正確な表現は、この直線が座標空間\(\mathbb{R}^3\)に描画されているという前提のもと、
\[\exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t\mathbf{a}\]
ということなるわけです。
ベクトル値関数とその値域
1つ前のセクションでは、パラメータ(媒介変数)の実態を明確にしつつ、存在量化子が付与された3変数述語
\[R(x_1,x_2,x_3):=\;\exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t\mathbf{a}\]
という観点から直線のパラメータ表示を厳密に捉え直しました。このセクションでは、視点を変えて、ベクトル値関数とその値域という視点から直線のパラメータ表示を厳密に捉えていきます。
まず結論として、直線のパラメータ表示は、以下のベクトル値関数
\[\mathbf{x}: \mathbb{R} \rightarrow \mathbb{R}^3;\; t \mapsto \mathbf{p} + t\mathbf{a}\]
の値域\(\text{ran}(\mathbf{x})\)としても解釈可能であり、\(\text{ran}(\mathbf{x})\)の全ての元(点)を座標空間(\(\mathbb{R}^3\))にプロットすれば、それが、点\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}(\neq \mathbf{0})\)を持つ直線になります。
具体的に見ていきましょう。ベクトル値関数
\[\mathbf{x}: \mathbb{R} \rightarrow \mathbb{R}^3;\; t \mapsto \mathbf{p} + t\mathbf{a}\]
は、何らかの実数\(t\)をインプットすると、3次元ベクトル\(\mathbf{p} + t\mathbf{a}\)をただ1つアウトプットする関数です。より簡潔に
\[\mathbf{x}(t) = \mathbf{p} + t\mathbf{a}\]
と表すこともできます。例えば、ある一つの実数\(c_1\)をインプットすれば、3次元ベクトル
\[\mathbf{x}(c_1) = \mathbf{p} + c_1\mathbf{a}\]
がアウトプットされます(図_2-1)。
 図_2-1
図_2-1
さらに、\(c_2,c_3,\ldots, c_n, \ldots\)と次々とインプットすると、3次元ベクトル\(\mathbf{x}(c_2),\mathbf{x}(c_3),\ldots , \mathbf{x}(c_n), \ldots\)が次々にアウトプットされていき、やがて直線を形成する訳ですが、、、、、、、(図_2-2)
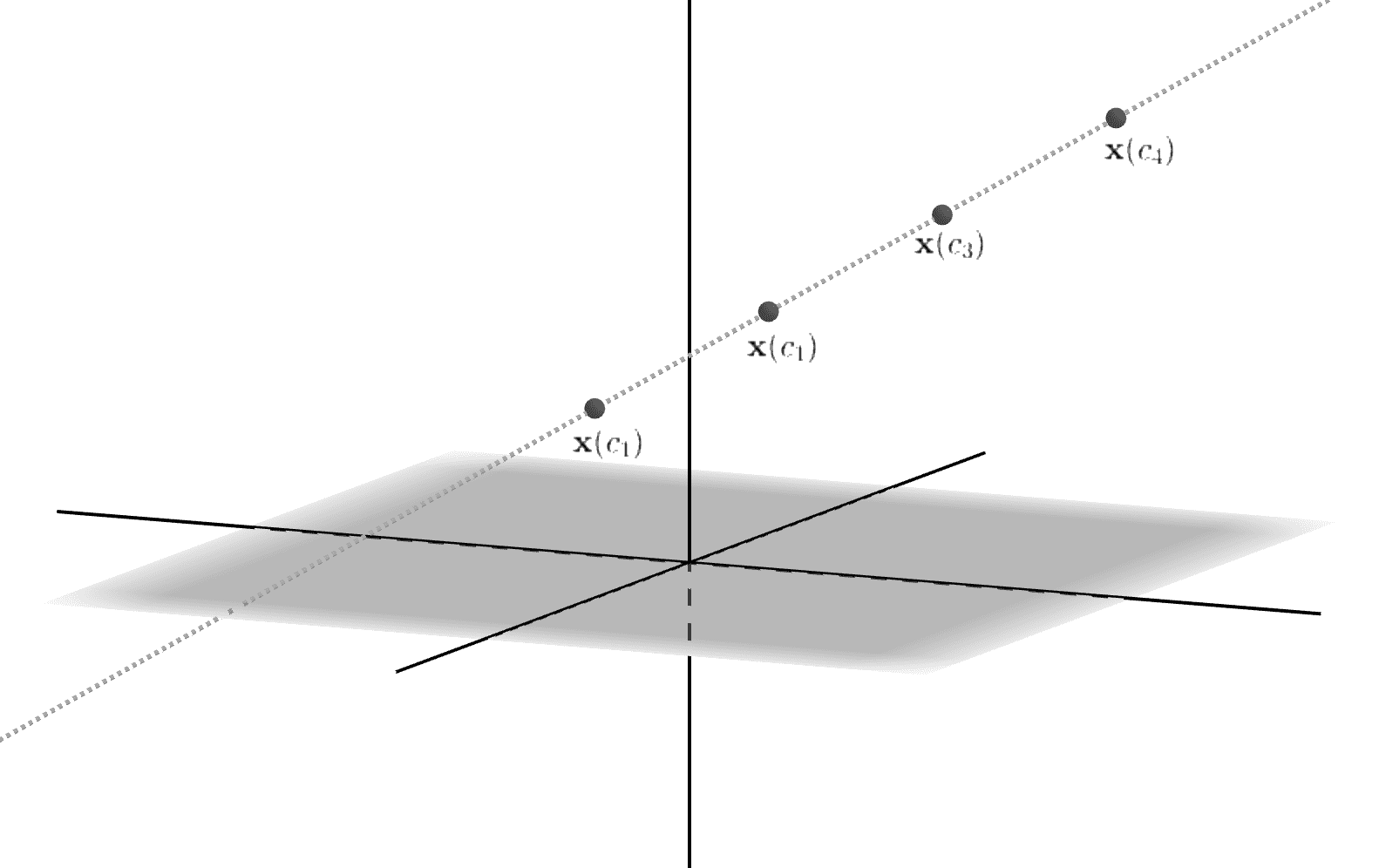 図_2-2
図_2-2
ここで視点を切り替え、この関数の値域\(\text{ran}(\mathbf{x})\)を考えてみると、写像の値域の一般的な定義から
\[ \text{ran}(\mathbf{x}) = \{\mathbf{x}\;|\; \exists t \in \mathbb{R},\; \mathbf{x} = \mathbf{p}+t\mathbf{a}\}\]
です。ここで、\(\text{ran}(\mathbf{x})\)の元を規定する条件が、
\[\exists t \in \mathbb{R},\; \mathbf{x} = \mathbf{p}+t\mathbf{a}\]
である点に注目してください。これは、先に解説した存在量化子が付与された3変数述語
\[R(x_1,x_2,x_3):=\;\exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t\mathbf{a}\]
としての直線のパラメータ表示に他なりません。もうこの時点で、
\[\mathbf{x}: \mathbb{R} \rightarrow \mathbb{R}^3;\; t \mapsto \mathbf{p} + t\mathbf{a}\]
というベクトル値関数の値域\(\text{ran}(\mathbf{x})\)が、点\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}(\neq \mathbf{0})\)を持つ直線に等しいことが分かったわけですが、\(\text{ran}(\mathbf{x})\)は、さらに以下のようにも変形できます。
\[\text{ran}(\mathbf{x})=\{\mathbf{p}+t\mathbf{a} \;|\; t \in \mathbb{R}\}\]
このように\(\text{ran}(\mathbf{x})\)を表現すれば、本記事の一番最初で説明した曖昧な形での直線のパラメータ表示
\[\mathbf{p}+t\mathbf{a}\;\;\; (t \in \mathbb{R})\]
にグッと近づきました。というよりも、これこそが、「変数\(t\)を実数\(\mathbb{R}\)上を任意に動かした(\(t \in \mathbb{R}\))ときの、全ての\(\mathbf{p}+t\mathbf{a}\)から成る集合」ということの厳密な定式化というわけです。
直線のパラメータ表示と関連する諸概念
このセクションでは、直前のセクションで解説した直線のパラメータ表示の厳密な定義を元にしつつ、直線のパラメータ表示と密接に関連する
- 線形代数の1次元部分空間
- 最適化理論の凸結合
という2つの概念を直線のパラメータ表示と関係付ながら解説していきます。
1次元線形部分空間
点\(\mathbf{p}\)を通り、方向ベクトル\(\mathbf{a}\)をもつ直線のパラメータ表示は、3項関係として
\[R(x_1,x_2,x_3):= \exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t\mathbf{a}\]
ということでした。ここで、\(\mathbf{p}=\mathbf{0}\)とすれば、
\[R'(x_1,x_2,x_3):= \exists t \in \mathbb{R},\; \mathbf{x}=t\mathbf{a}\]
という3項関係ですが、この3項関係が真になる全ての\(\mathbf{x}=(x_1,x_2,x_3)\)を集めた集合、つまり、\(R'(x_1,x_2,x_3)\)の真理集合は
\[\{\mathbf{x}\;|\; \exists t \in \mathbb{R},\; \mathbf{x}=t\mathbf{a}\}\]
であり、その幾何学的な解釈は原点\(\mathbf{0}\)を通り、方向ベクトル\(\mathbf{a}\)をもつ直線です。さらに、これは
\[\{t\mathbf{a}\;|\; t \in \mathbb{R}\}\]
と変形できますが、これは、線形代数における\(\mathbf{a}\)を基底ベクトルとした1次元線形部分空間に他なりません。
これより、\(\mathbf{a}\)を基底とする1次元線形部分空間は、原点\(\mathbf{0}\)を通り、方向ベクトル\(\mathbf{a}\)を持つ直線として解釈できることが分かります。

ところで、任意の\(\mathbf{p}\neq \mathbf{0}\)に対して、直線\(\{t\mathbf{a}\;|\; t \in \mathbb{R}\}\)が\(\mathbf{p}\)を通るには、直線を\(\mathbf{p}\)だけ平行移動して、
\[\{\mathbf{p}+t\mathbf{a}\;|\; t \in \mathbb{R}\}\]
ですが、この直線から1つ矢印としての幾何ベクトル\((\mathbf{p}+\mathbf{a})-\mathbf{p}\)を抽出します。このベクトルは、始点が\(\mathbf{p}\)、終点\(\mathbf{p}+\mathbf{a}\)です。(図_3-1)
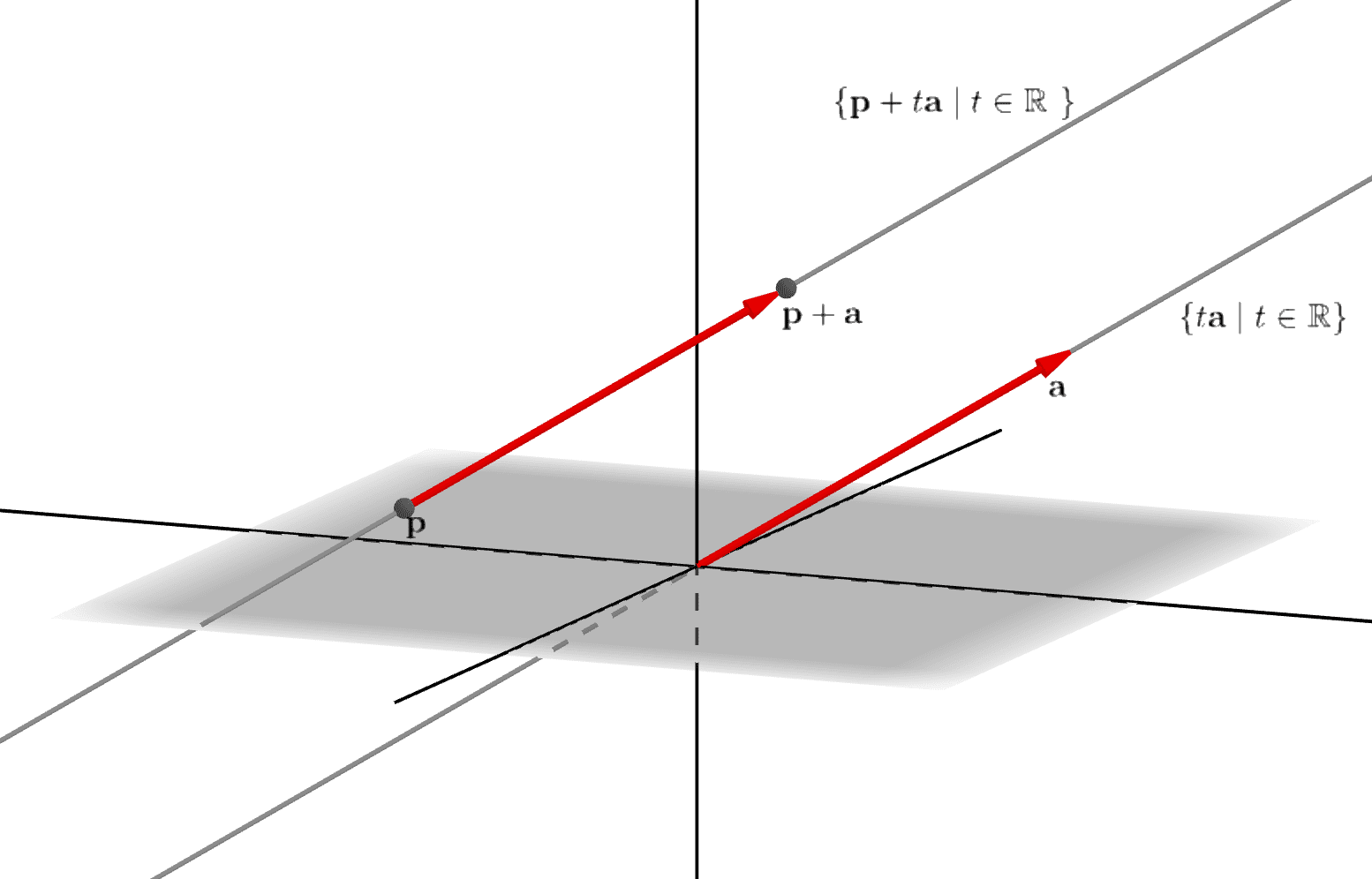 図_3-1
図_3-1
ここで、幾何ベクトルには、「向きと大きさが同じなら、どこに位置しようとも、同じベクトルとして扱う」という同値関係が適用されます。これは、幾何ベクトルの終点と始点の差分によって判定され、\((\mathbf{p}+\mathbf{a})-\mathbf{p}\)のケースでは、
\[(\mathbf{p}+\mathbf{a})-\mathbf{p} = \mathbf{a}\]
ですが、この結果は、直線\(\{t\mathbf{a}\;|\; t \in \mathbb{R}\}\)から1つ幾何ベクトル\(\mathbf{a}\)を取り出したとすれば、幾何ベクトルの同値関係という視点で見れば、2つの直線
\[\{\mathbf{p}+t\mathbf{a}\;|\; t \in \mathbb{R}\}\;\; \text{と}\;\; \{t\mathbf{a}\;|\; t \in \mathbb{R}\}\]
は同値、つまり、全くの等価ということになります。ここから、線形代数を幾何ベクトルとして捉えてみると、ベクトルの「位置」情報を完全に無視して、「向き」だけにフォーカスして議論していることが分かります。
つまり、線形代数とは、具体的な幾何学的要素(位置や始点・終点)には一切目を向けず、(抽象的な)方向やスカラー倍の構造を考察する学問であると言えそうです。
線分と凸結合
ここまでの議論により、2点\(\mathbf{p},\mathbf{q}\)を通る直線は、\(\mathbb{R}^3\)の部分集合\(D\)として、
\begin{align*}
D &= \{\mathbf{x}\;|\; \exists t \in \mathbb{R},\; \mathbf{x}=\mathbf{p}+t(\mathbf{q}-\mathbf{p})\} \\
&= \{\mathbf{p}+t(\mathbf{q}-\mathbf{p}) \;|\; t \in \mathbb{R}\}
\end{align*}
と表されるのでした。(図_3-2)
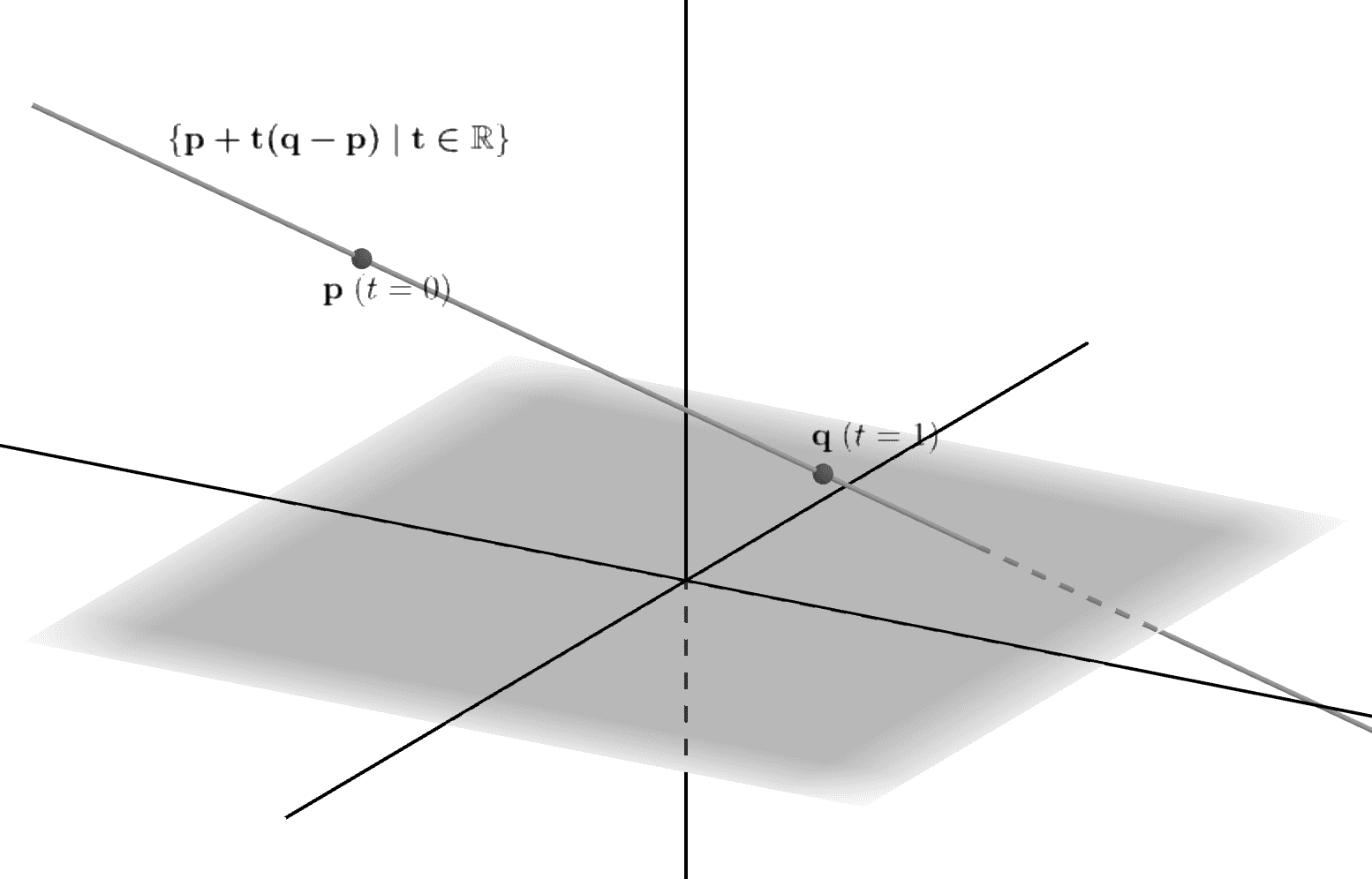 図_3-2
図_3-2
このとき、\(t=0\)で\(\mathbf{p}\)、\(t=1\)で\(\mathbf{q}\)という事実を考慮しつつ、パラメータ\(t\)の変域を\(\mathbb{R}\)全体から\([0,1]\)に制限します。このときの部分集合を\(D’\)とすれば、
\[D’ = \{\mathbf{p}+t(\mathbf{q}-\mathbf{p}) \;|\; t \in [0,1]\}\]
です。この\(D’\)を「2点\(\mathbf{p},\mathbf{q}\)を端点とする線分」といいます。(図_3-3)
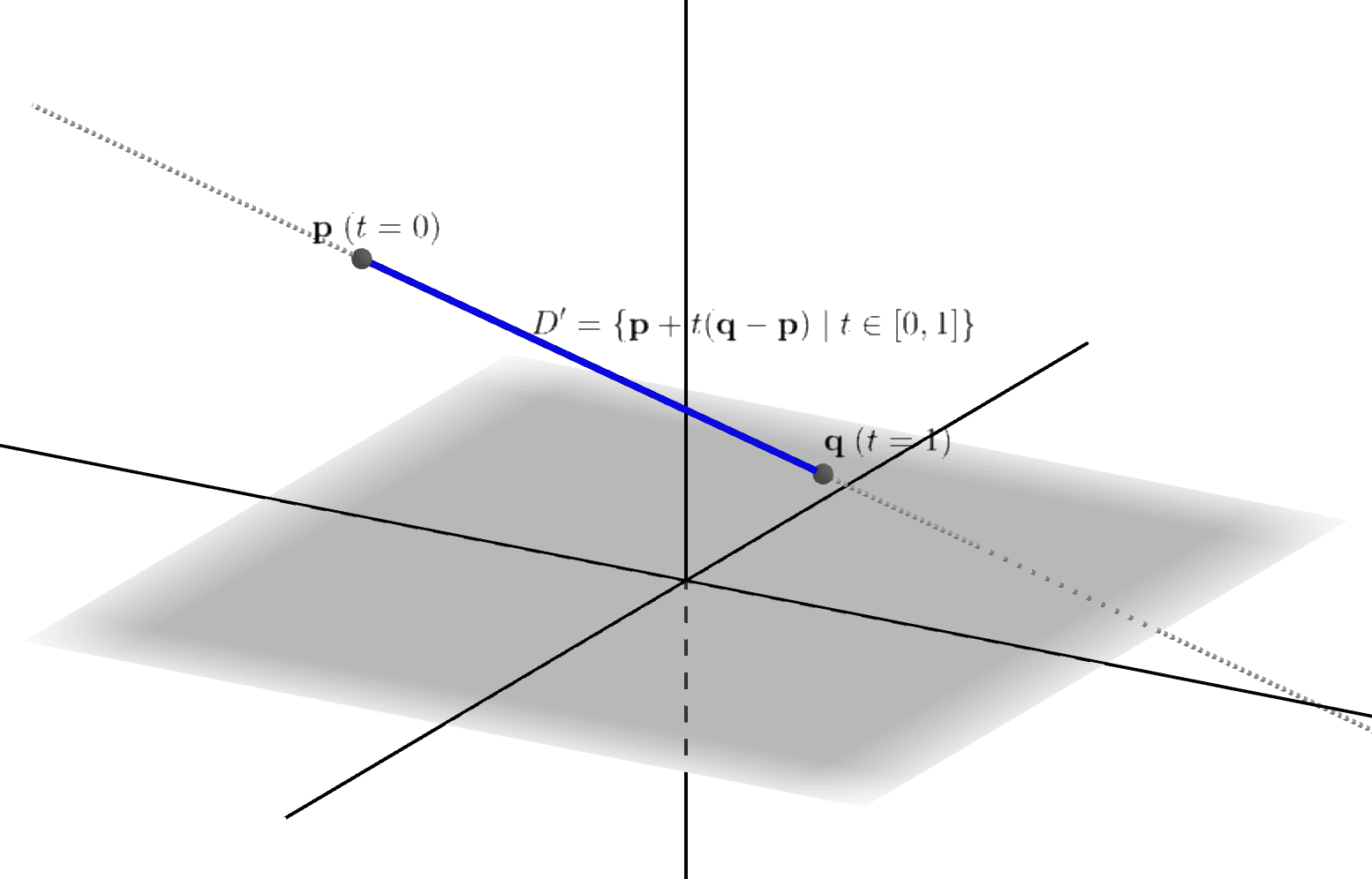 図_3-3
図_3-3
つまり、2点を通る線分は、2点を通る直線のパラメータ表示において、パラメータの変域を\([0,1]\)に制限することで得られるわけです。
また、
\begin{align*}
\mathbf{p}+t(\mathbf{q}-\mathbf{p}) &= \mathbf{p} + t\mathbf{q} – t\mathbf{p} \\
&= t\mathbf{q} + (1-t)\mathbf{p} \\
\end{align*}
であるから、\(D’\)は、
\[D’ = \{t\mathbf{q} + (1-t)\mathbf{p}\;|\; t \in [0,1]\}\]
とも表せます。ここで、パラメータ\(t\)を、\(\mathbf{q}\)の係数\(t\)、\(\mathbf{p}\)の係数\(1-t\)という視点でみたとき、
\[\begin{cases}
0 \leq t \leq 1 \\
t + (1-t) = 1
\end{cases}\]
が当然ながら成り立っています。そこで、
\[t = \lambda_1,\;\; 1-t = \lambda_2\]
とおけば、
\[\lambda_1 + \lambda_2 = 1\]
です。また、\(0 \leq t \leq 1\)より、
\[0 \leq \lambda_1 \leq 1\]
であり、\(t = 1-\lambda_2\)より、\(0 \leq 1-\lambda_2 \leq 1\)、つまり、
\[0 \leq \lambda_2 \leq 1\]
です。以上、一連の置き換えによって、\(D’\)は、
\[\begin{cases}
0 \leq \lambda_i \leq 1 \;\; (i=1,2) \\
\lambda_1 + \lambda_2 = 1
\end{cases}\]
を満たす点\(\mathbf{x}=\lambda_1 \mathbf{q}+ \lambda_2 \mathbf{p}\)の集合としても表現できます。また、特にこのように表された2点\(\mathbf{p},\mathbf{q}\)を端点とする線分を2点\(\mathbf{p},\mathbf{q}\)を端点とする「凸結合」と言います。凸結合は、最適化理論などで非常に重要な役割を果たす概念・ツールです。
参考文献
本記事は以下の書籍をもとに執筆しています。
S.ラング 続 解析入門
直線のパラメータ表示の直観的な理解のための解説は、本書を参考にしました。また、直線のパラメータ表示を2パターンに分類するのも、この本からアイディアを得ています。
論理と集合から始める数学の基礎
直線のパラメータ表示の厳密な導出と定義は、本書をもとにしています。数学を極めたい人は、絶対に読むべき素晴らしい本です。



