本記事では、2つのベクトル\(\mathbf{u},\mathbf{v}\)に対して、特に\(\mathbf{u}\)が正規化されているケース(\( \|\mathbf{u} \|=1 \))の内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)の意味、解釈、活用方法を解説します。
一般的に、2つのベクトル\(\mathbf{u},\mathbf{v}\)の内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)は、何ら分類もされず一括りにされてしまうことが大半です。
しかし、これを以下3パータンで分類すると、理論的な見通しがよくなり、内積という操作に対してより具体的なイメージが持てるようになると考えます。
この記事では、この分類に基づき、2(中段)のケースを解説していくわけですが、本文の要点は以下の通りです。
2つのベクトル\(\mathbf{u},\mathbf{v}\)に対して、特に\(\mathbf{u}\)が正規化されているケースでは、内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)は、
- 幾何学的に「\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影」として、\( \mathbf{u} \)方向への\( \mathbf{v} \)の配分割合と解釈でき、
- 従って、「\(\mathbf{u}\)方向に対する\(\mathbf{v}\)の影響力」の指標として活用できる
また、記事の最後には、この2パターンの内積の応用例として、
- 方向微分係数
- 主成分分析における主成分
を取り上げました。
なお、パターン1,3に関しては、『コーシー・シュワルツ不等式とその証明 〜内積/コサイン/角度との関連〜』にて解説しているので参考にしてください。
内積と射影の関係
まずは、内積と射影の関係を明確にしていきます。
具体的には、2つのベクトル\(\mathbf{u},\mathbf{v}\)に対して、\(\mathbf{u}\)が正規化されている場合の内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)が、「\(\mathbf{u}\)方向に沿う\(\mathbf{v}\)の射影」として幾何学的に解釈できることを確認していきます。
ベクトル\(\mathbf{u}\)に沿うベクトル\(\mathbf{v}\)の射影
まず最初に、「ベクトル\(\mathbf{u}\)に沿うベクトル\(\mathbf{v}\)の射影」という概念を導入します。
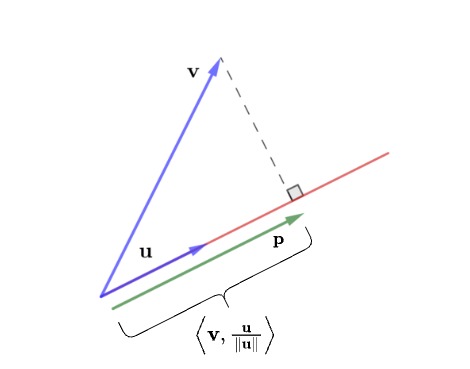
\(\mathbf{u},\mathbf{v}\) は、平行でなく、かつ、ゼロベクトルでもない2つの異なるベクトルとし、また、\(\mathbf{u}\)に関しては、\(\|\mathbf{u}\|=1\)であるとします。
ここで、\(\mathbf{u}\)を任意にスカラー倍することで生成される直線上（赤線）へ、\(\mathbf{v}\)から垂線を下ろすと、垂線と直線の交点を終点とし、かつ \(\mathbf{u}\) と平行関係にあるベクトル \(\mathbf{p}\) が定まります。
これより、\(\mathbf{p}\) は、あるスカラー \(c\) が存在して、\(\mathbf{p} = c\mathbf{u}\) と表せます。この\(c\)を、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分といい、また、\(\mathbf{p}\)を、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影、または、射影ベクトルといいます。
一方で、これと同時に、\(\mathbf{v} – \mathbf{p}\) というベクトルも生成され、これは\(\mathbf{u}\) と直交します。なぜなら、\( \mathbf{v} \) から\(\mathbf{u} \) への垂線と平行だからです。
以上の仮定をもとに、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c\)と \( \mathbf{u} \)に沿う\(\mathbf{v} \)の射影\( \mathbf{p} \) を求めていきます。
そして、これらが、\(\mathbf{v}\)と\(\mathbf{u}\)の内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)と、どのように関係しているのかを探っていきます。
射影の導出と内積との関係
まず、\(\mathbf{v} – \mathbf{p}\)は\(\mathbf{u}\)と直交するので、これらの内積は0になります。
\[
\langle \mathbf{u}, \mathbf{v} – \mathbf{p} \rangle = 0
\]
次に、\(\mathbf{p} = c\mathbf{u}\) なので、これを上式に代入します。その上で、以下のように式変形して、\(c\)を求めます。
\begin{align}
\langle \mathbf{u}, (\mathbf{v} – c \mathbf{u} ) \rangle&= 0 \\
\langle \mathbf{u} , \mathbf{v} \rangle – c\langle \mathbf{u} , \mathbf{u}\rangle &= 0 \\
c\| \mathbf{u}\|^2 &= \langle \mathbf{u} , \mathbf{v} \rangle \\
c &= \frac{\langle \mathbf{u} , \mathbf{v} \rangle}{\| \mathbf{u}\|^2}
\end{align}
\(\langle \mathbf{u},\mathbf{u}\rangle = \|\mathbf{u}\|^2\)を用いましたが、\(\|\mathbf{u}\| = 1\)という仮定より、\(\|\mathbf{u}\|^2 = 1\)。従って、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c\)は、
\[c = \langle \mathbf{u} , \mathbf{v} \rangle\]
です。これより、\(\mathbf{v}\)と正規化された\(\mathbf{u}\)の内積は、「\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c\)」として解釈できることが分かります。
さらに、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影は、\(\mathbf{p} = c\mathbf{u}\)より
\[\mathbf{p} = \langle \mathbf{u} , \mathbf{v} \rangle \mathbf{u}\]
ですが、ここで、射影ベクトル\(\mathbf{p}\)のノルムを求めると、
\begin{align}
\|\mathbf{p}\| &= \|\langle \mathbf{v}, \mathbf{u}\rangle \mathbf{u}\| \\
&= |\langle \mathbf{v}, \mathbf{u}\rangle|\|\mathbf{u}\| \\
&= |\langle \mathbf{v}, \mathbf{u}\rangle| \\
&= |c|
\end{align}
つまり、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c\)は、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影ベクトルの符号(向き)を考慮したノルムに一致します。\(\mathbf{u}\)と同じ方向なら\(c\)は正で、\(\mathbf{u}\)と反対方向なら\(c\)は負となります。
以上より、内積と射影の関係として以下の結論が得られます。本セクションの要点としてまとめておきましょう。
\(\mathbf{v}\)と正規化された\(\mathbf{u}\)の内積は、「\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c\)を与え、これは、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影ベクトルの符号を考慮したノルムに対応する
【補足】方向ベクトルの正規化が仮定されない場合
一つ補足をしておきます。
ここまでは、\( \mathbf{u} \)が正規化されていることを仮定して話を進めてきたので、\( \mathbf{u} \) に沿う\( \mathbf{v} \)の成分\( c\) は、\( \mathbf{v} \) と\( \mathbf{u} \) の内積というシンプルな形で、\( c = \langle \mathbf{v}, \mathbf{u}\rangle\)と表現できました。
しかし、\( \mathbf{u} \)の正規化を仮定しない場合、 \( \mathbf{u} \) に沿う\( \mathbf{v} \)の成分\( c\) は、
\[c = \frac{\langle \mathbf{v} , \mathbf{u} \rangle}{\|\mathbf{u} \|^2}\]
と、\( \mathbf{v} \) と\( \mathbf{u} \) の内積という形では表せません。ただし、射影ベクトル\( \mathbf{p} \)のノルムに関しては、
\begin{align}
\|\mathbf{p}\| &= \left\|\frac{\langle \mathbf{v}, \mathbf{u}\rangle}{\|\mathbf{u}\|^2} \mathbf{u}\right\|\\
&=\frac{|\langle \mathbf{v}, \mathbf{u}\rangle|}{\|\mathbf{u}\|^2} \|\mathbf{u}\| \\
&= \frac{|\langle \mathbf{v}, \mathbf{u}\rangle|}{\|\mathbf{u}\|}\\
&=\left|\left\langle \mathbf{v}, \frac{\mathbf{u}}{\|\mathbf{u}\|}\right\rangle \right|
\end{align}
と、\( \mathbf{v} \)と正規化された\( \mathbf{u} \)の内積として求まります。\( \mathbf{u}/\|\mathbf{u}\|\)は、ノルムが1の\( \mathbf{u} \)、つまり正規化された\(\mathbf{u}\)であることに注意しましょう。
以上を考慮すると、本セクションの要点は以下のように修正されます。
\(\mathbf{v}\)と正規化された\(\mathbf{u}\)の内積で求まるのは、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影ベクトルの符号(向き)を考慮したノルム。
上図の場合、︸ の範囲が、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影ベクトルの符号(向き)を考慮したノルムで、これが、\( \left\langle \mathbf{v} , \frac{\mathbf{u} }{\|\mathbf{u} \|}\right \rangle\)で求まります。この例では、\( \mathbf{p} \)は、\( \mathbf{u} \)と同じ向きなので、\( \left\langle \mathbf{v} , \frac{\mathbf{u} }{\|\mathbf{u} \|}\right \rangle > 0\)です。
少しややこしいですが、最後に紹介する方向微分係数は、この形で導出されます。
以降では、話をシンプルにするために、常に\( \mathbf{u} \)は正規化されている、従って、\( c= \langle \mathbf{u}, \mathbf{v}\rangle\) として進めていきます。
角度とコサインの視点から見た内積と射影
このセクションでは、角度とコサインの視点から\( c= \langle \mathbf{u}, \mathbf{v}\rangle\)に対してより明確な意味付けをしていきます。
まず、\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)を内積の１つの表現方法を用いて、
\[c = \langle \mathbf{u} , \mathbf{v} \rangle = \|\mathbf{v} \|\, \|\mathbf{u} \| \cos \theta\]
と表します。ここで、\(\theta\)は\( \mathbf{v} \)と\( \mathbf{u}\)のなす角です。ただし、今は\(\|\mathbf{u}\|=1\)という仮定をおいているので、
\[c = \langle \mathbf{u} , \mathbf{v} \rangle = \|\mathbf{v} \|\,\cos \theta\]
となります。\(\cos \theta\)は、\( \mathbf{v} \)と\( \mathbf{u}\)のなす角\(\theta \)に応じて、\(-1 \leq \cos \theta \leq 1\)。
これより、\( \mathbf{v} \)と正規化した\( \mathbf{u} \)の内積、すなわち、\(\mathbf{u}\)に沿う\(\mathbf{v}\)の成分\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)とは、\(\mathbf{u}\)と\(\mathbf{v}\)の位置関係を考慮に入れた、\( \mathbf{v} \)のノルム(大きさ）を全体量としたときの\( \mathbf{u} \)方向への配分割合と解釈できます。
\(\mathbf{u}\)と\(\mathbf{v}\)の位置関係、つまり、\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)の符号は以下のように定まります。
\begin{cases}
0 \leq \theta < \pi/2 \rightarrow c =\langle \mathbf{u} , \mathbf{v}\rangle > 0 \\
\pi/2 < \theta \leq \pi \rightarrow c = \langle \mathbf{u} , \mathbf{v}\rangle < 0 \end{cases}
以上をもとにすると、\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)の最大値、最小値、また、これらの値をとるときの\(\mathbf{u}\)と\(\mathbf{v}\)の位置関係は以下のようになります。
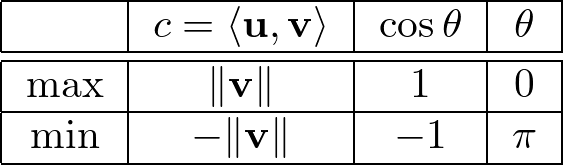
すなわち、\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)の最大値は、\( \mathbf{u} \)が\(\mathbf{v}\)と同じ方向を向いているとき、\(\|\mathbf{v}\|\)をとります。これは、\( \mathbf{v} \)のノルムをどの方向にも配分せず、純粋な\(\mathbf{v}\)そのものとして扱うことに相当します。
対して、最小値は、\( \mathbf{v} \)が\(\mathbf{u}\)と真反対の方向を向いているとき、\(-\|\mathbf{v}\| \)をとります。
さらに、\( \cos \theta = 0 \)、つまり、\(\theta = \pi/2\) で\( \mathbf{u} \)と\(\mathbf{v}\)が直交しているとき、\(c = \langle \mathbf{u} , \mathbf{v}\rangle = 0\)となります。\( \mathbf{v} \)と\( \mathbf{u} \)が直交関係にあるとき、\( \mathbf{u} \)方向への\( \mathbf{v} \)の配分は一切ない、ということです。直交に関しては『ベクトルの直交とピタゴラスの定理 〜MSEのバイアス・バリアンス分解との関連〜』でより詳細に解説しているので参考にして下さい。
なお、ここまでの考察を\(\cos \theta\)を使わずに表すと、
\[|\langle \mathbf{u} , \mathbf{v}\rangle| \leq \|\mathbf{v}\|\]
とコーシー・シュワルツの不等式で\(\|\mathbf{u}\| = 1\)のケースが導出され、これを絶対値記号を取って表せば、
\[-\|\mathbf{v}\| \leq \langle \mathbf{u} , \mathbf{v}\rangle \leq \|\mathbf{v}\|\]
となり、\(c = \langle \mathbf{u} , \mathbf{v}\rangle\)のとりうる範囲がより明確に示されます。
影響力の指標としての内積と射影
このセクションでは、ここまでの議論をもとに、\(\mathbf{v}\)と正規化された\(\mathbf{u}_i\)の内積\(\langle \mathbf{u}_i , \mathbf{v}\rangle\)が、「\(\mathbf{u}_i\)方向に対する\(\mathbf{v}\)の相対的な影響力」の指標として機能することを見ていきます。
今、\(\mathbf{u}_1\)に対して、\(\mathbf{u}_1\)に沿う\(\mathbf{v}\)の成分\(\langle \mathbf{u}_1 , \mathbf{v}\rangle\)を求めれば、それは、\(\mathbf{u}_1\)に沿う\(\mathbf{v}\)の射影ベクトル\(\mathbf{p}_1\)の符号を考慮したノルムです。
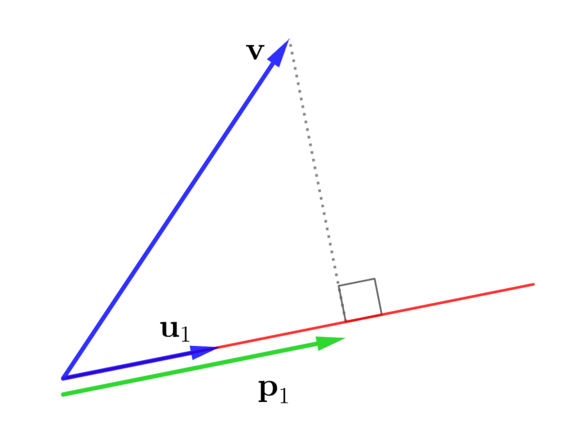\( \mathbf{p}_1 \)は \( \mathbf{u}_1 \)方向に沿う\(\mathbf{v} \)の射影ベクトル一方で、\(\mathbf{u}_1\)とは別の方向を向いた\(\mathbf{u}_2\)というベクトルを用意し、\(\mathbf{u}_2\)に沿う\(\mathbf{v}\)の成分\(\langle \mathbf{u}_2 , \mathbf{v}\rangle\)を求めれば、それは、\(\mathbf{u}_2\)に沿う\(\mathbf{v}\)の射影ベクトル\(\mathbf{p}_2\)の符号を考慮したノルムとなります。
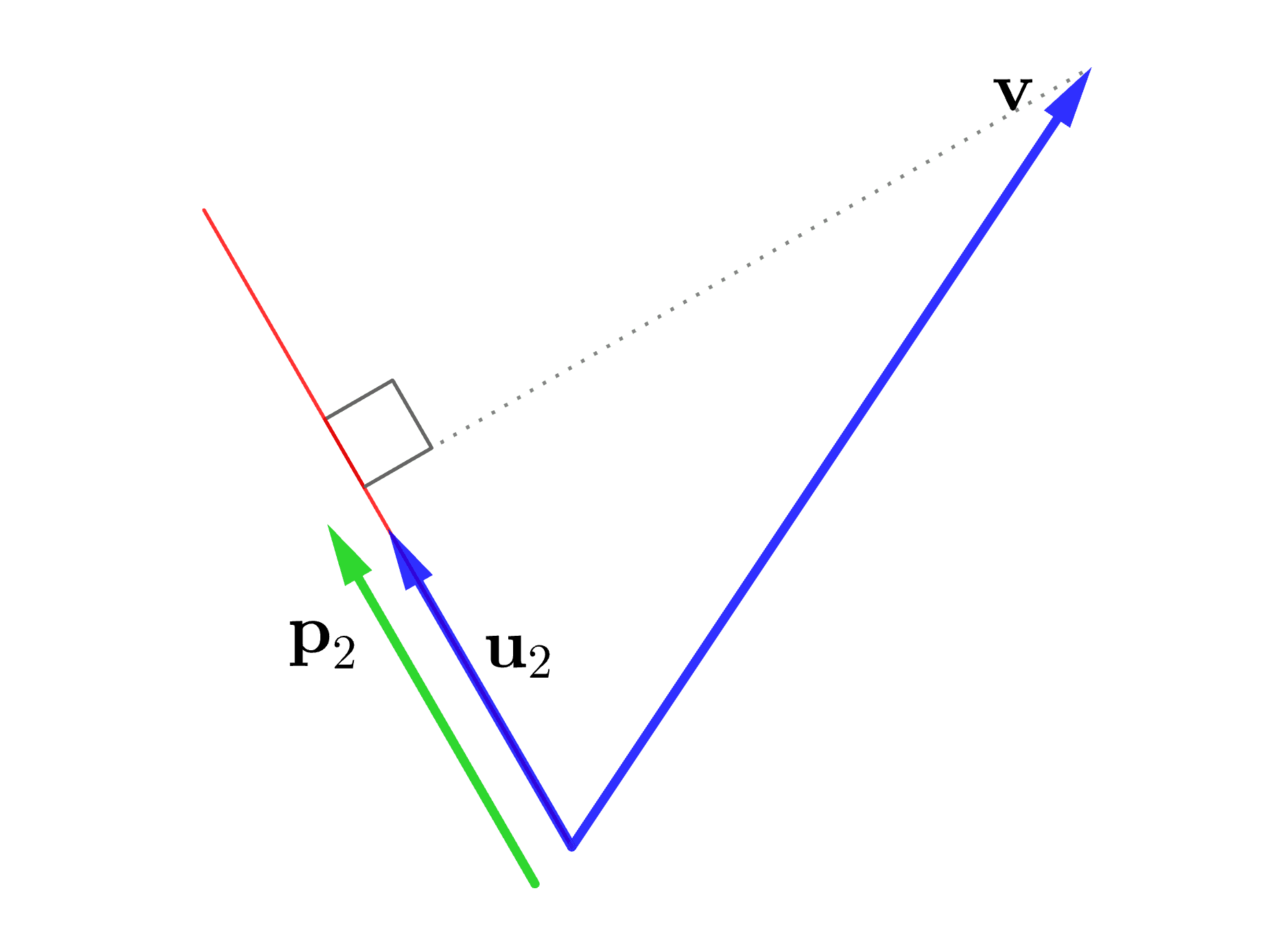\( \mathbf{p}_2 \) は、\( \mathbf{u}_2 \)方向に沿う\(\mathbf{v} \)の射影ベクトルこのとき、\(\langle \mathbf{u}_1 , \mathbf{v}\rangle\)と\(\langle \mathbf{u}_2 , \mathbf{v}\rangle\)を比較して、\(\mathbf{v}\)が相対的にどちらの方向に影響力を持っているか、すなわち、\(\|\mathbf{v}\|\)は、相対的にどちらの方向により多く配分されているかを考察することは、\(\mathbf{v}\)の性質を探る上で妥当かつ効果的な方法と言えます。
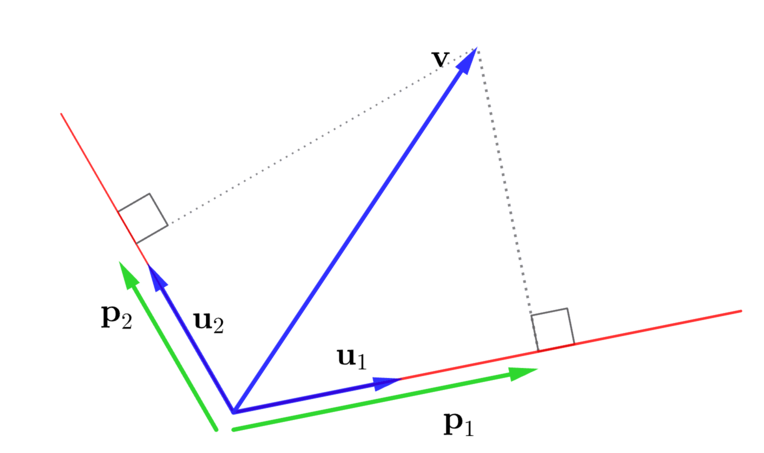
上図の例では、\(\|\mathbf{v}\|\)は、\(\mathbf{u}_2\)方向よりも\(\mathbf{u}_1\)方向に対して、より多く配分されているから、従って、\(\mathbf{v}\)は、\(\mathbf{u}_2\)方向と比べて\(\mathbf{u}_1\)方向に対して相対的に影響力を持っている」という解釈ができます。
内積と射影の応用例
ここまでで、2つのベクトル\(\mathbf{u},\mathbf{v}\)に対して、特に\(\mathbf{u}\)が正規化されているケースでは、内積\(\langle \mathbf{u}, \mathbf{v}\rangle\)が、幾何学的に「\(\mathbf{u}\)に沿う\(\mathbf{v}\)の射影」として、\( \mathbf{u} \)方向への\( \mathbf{v} \)の配分割合と解釈でき、従って、「\(\mathbf{u}\)方向に対する\(\mathbf{v}\)の影響力」の指標として活用できる、ということを見てきました。
最後のセクションでは、内積のこの活用がどのように応用されているのかを以下2つの例を挙げてみていきます。
- 方向微分係数
- 主成分分析の主成分
方向微分係数
n変数関数\( f(\mathbf{x} ):\mathbb{R}^n \rightarrow \mathbb{R}\) が\( \mathbf{p} \)で全微分可能であるとき、関数\(f \) の\( \mathbf{p} \)での勾配ベクトル\(\nabla f(\mathbf{p} ) \)と関数\( g: \mathbb{R}^n \rightarrow \mathbb{R}\)が存在して、任意の方向ベクトル\(\mathbf{h} \in \mathbb{R}^n \) に対して、
\[\begin{cases}
f(\mathbf{p} +\mathbf{h}) – f(\mathbf{p} ) = \nabla f(\mathbf{p} ) \cdot \mathbf{h} + \|\mathbf{h}\|g(\mathbf{h}) \\
\lim_{\|\mathbf{h}\|\rightarrow 0}\:\:\: g(\mathbf{h})=0
\end{cases}
\]
が成り立ちます。ここで、\( \nabla f(\mathbf{p} ) \cdot \mathbf{h}\)は、\( \nabla f(\mathbf{p} )\)と\( \mathbf{h}\)の内積です。本記事では、これまで内積をブラケット記号\(\langle \: \rangle\)で表してきましたが、微積分の文脈では、ドット記号\( \cdot\)がよく使われるので、ここではドット記号で内積を表します。
話を戻して、全微分可能なときに得られる上式ですが、これを1つにまとめると、以下の等式が得られます。
\[\lim_{\|\mathbf{h}\|\rightarrow 0} \frac{f(\mathbf{p} +\mathbf{h}) – f(\mathbf{p} )}{\|\mathbf{h}\|} = \frac{\nabla f(\mathbf{p} ) \cdot \mathbf{h}}{\|\mathbf{h}\|} \]
左辺は、関数\(f\)の点\(\mathbf{p} \)における\(\mathbf{h}\)方向への平均変化率の極限です。つまり、\(\mathbf{h}\)方向でみたときの\(f\)の点\(\mathbf{p}\)での局所的な変化率です。
一方で右辺
\[\frac{\nabla f(\mathbf{p} ) \cdot \mathbf{h}}{\|\mathbf{h}\|}\]
は、\(\mathbf{h} \)方向への\( f\)の点\(\mathbf{p} \) での方向微分係数と呼ばれていますが、よく形を見てみましょう。
これは、正規化された方向ベクトル\(\mathbf{h} \)と\( f\)の点\(\mathbf{p} \) での勾配ベクトル\(\nabla f(\mathbf{p} ) \) の内積です。
つまり右辺は、\(\mathbf{h} \)方向に沿う\( f\)の点\(\mathbf{p}\)での勾配ベクトル\(\nabla f(\mathbf{p} ) \)全体量の配分割合という解釈ができます。
関数\(f\)の勾配ベクトル\(\nabla f(\mathbf{p})\)は、\(f\)の点\(\mathbf{p}\)での局所的な変化率情報を保有したベクトルですが、点\(\mathbf{p}\)と言っても、様々な方向に応じて、\(f\)の変化率は異なります。
しかし、一旦方向を\(\mathbf{h}\)と決めたならば、この\(\mathbf{h}\)方向には、どれだけ\(\nabla f(\mathbf{p})\)を配分しているか？つまり、
\[\nabla f(\mathbf{p}) \cdot \frac{\mathbf{h}}{\|\mathbf{h}\|}= \|\nabla f(\mathbf{p})\|\; \cos \theta\]
により、\(\mathbf{h}\)方向への\(\|\nabla f(\mathbf{p})\|\)の配分割合、つまり、関数\(f\)の点\(\mathbf{p}\)での\(\mathbf{h}\)方向に限定した局所的な変化率を、射影ベクトルの向き(符号)を加味したノルムとして抽出できるというわけです。
主成分分析における主成分
\( \mathbb{R}^n\)において、\(\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_n\)を基底とする正規直交基底を想定します。つまり、各基底ベクトルには
\[\begin{cases}
\|\mathbf{u}_i\| = 1 \\
\langle \mathbf{u}_i, \mathbf{u}_j \rangle = 0 \:\:(i \neq j)
\end{cases}\]
という性質・関係が成立しています。このとき、任意のベクトル\(\mathbf{x} \in \mathbb{R}^n \)は、基底の線形結合
\[
\mathbf{x} = c_1 \mathbf{u}_1 + c_2 \mathbf{u}_2 + \cdots + c_n \mathbf{u}_n
\]
によって一意に表されるわけですが、このとき、基底ベクトル\( \mathbf{u}_k\) の係数\(c_k \)は、正規直交基底であることによって、
\[
c_k = \langle \mathbf{x}, \mathbf{u}_k \rangle
\]
で求まります(証明は省略します)。つまり、係数\( c_k\) は、\( \mathbf{x} \)と正規化された\( \mathbf{u}_k \)の内積で算出されるということです。
これより、係数\(c_k \)を、\(\mathbf{u}_k \)方向に沿う\( \mathbf{x} \)の配分割合(影響力)と解釈できます。 その上で、\( \mathbf{x} \)は、基底の線形結合で
\[
\mathbf{x} = \langle \mathbf{x}, \mathbf{u}_1 \rangle \mathbf{u}_1 + \langle \mathbf{x}, \mathbf{u}_2 \rangle \mathbf{u}_2 + \cdots + \langle \mathbf{x}, \mathbf{u}_n \rangle \mathbf{u}_n
\]
と表されますが、このとき、j番目以降の係数 \( \langle \mathbf{x}, \mathbf{u}_j \rangle,\; \langle \mathbf{x}, \mathbf{u}_{j+1} \rangle,\; \ldots,\; \langle \mathbf{x}, \mathbf{u}_n \rangle \) がある基準を下回るとき、\( \mathbf{x} \)は、これらの方向に対して、影響力が弱い、または、関連度が低いということになります。
そこで、これらの方向を捨ててしまって、
\[
\mathbf{x} \approx \langle \mathbf{x}, \mathbf{u}_1 \rangle \mathbf{u}_1 + \langle \mathbf{x}, \mathbf{u}_2 \rangle \mathbf{u}_2 + \cdots + \langle \mathbf{x}, \mathbf{u}_{j-1} \rangle \mathbf{u}_{j-1}
\]
と近似します。この一連のプロセスは次元削減と呼ばれ、これにより\( \mathbf{x} \)をより解釈が容易な低次元で扱うことができます。
これは主成分分析の中心にあるアイディアで、\( \mathbf{u}_i \)は分散共分散行列の固有ベクトルで、第i主成分軸といい、\( \langle \mathbf{x}, \mathbf{u}_k \rangle\)を、データベクトル\( \mathbf{x} \)の第k主成分と言います。
なお、 データベクトル\( \mathbf{x} \)は、「多変量データの行列・ベクトル表現と導出 〜多変量データ行列から分散共分散行列まで〜」 で解説していますが、多変量データ行列\( X\)の各行に相当します。また、分散共分散行列は、この多変量データ行列\( X\)から算出されます。
参考文献
本記事を執筆するにあたり、参考にした書籍や教材を挙げておきます。
なお、参考文献や教材の紹介にあたっては、アフィリエイトリンクを貼っていることをご承知ください。
ラング 続解析入門
本記事で採用した射影にまつわる用語や概念の定義(例えば、\(\mathbf{u} \)に沿う\( \mathbf{v} \)の成分など)は、この本に従いました。
多変数微積分とベクトル解析を区別せず統一的に扱った本です。
必要以上に厳密すぎず、また、理論展開にベクトルをメインに用いているので、\( \mathbb{R}^n\) 上での微分積分の各種概念や操作を直感的に学ぶことができる良書です。
線形代数の理論とPython による実践
線形代数の理論とPythonによる実践は、本ではなくUdemyの動画教材です。
射影と内積の関係式の導出は、この教材を参考にしました。
なお、一般的なUdemyの教材は、入門的な内容で深い理論を解説したものはほとんどありませんが、こちらの講座は、線形代数の基礎から応用までを深く、網羅的に解説していておすすめです。