この記事では、2つのベクトル\(\mathbf{a},\;\mathbf{b}\)が直交すること、すなわち、
\[\mathbf{a}\cdot \mathbf{b} = 0\]
という式の意味を、ピタゴラスの定理(三平方の定理)との関連を中心に解説します。
また記事後半では、2つのベクトルの直交の顕著な応用例として、データ分析や機械学習などでもしばしば登場する「平均二乗誤差(MSE)のバイアス・バリアンス分解」を取り上げました。
線形代数、多変数微積分、ベクトル解析を勉強している人はもちろんのこと、データ分析や機械学習を勉強している人にも役立つ内容なので是非参考にしてください。
「直交」という概念の直感的な解釈
直交という概念は、\(\mathbf{a}\)と\(\mathbf{b}\)の内積が0という内積の特別なケースとして定められます。
まず復習も兼ねて、\(\mathbf{a}\)と\(\mathbf{b}\)の内積の解釈に関して、以下の表用いて簡単に確認しておきましょう。より詳細な解説は『コーシー・シュワルツ不等式とその証明 〜内積/コサイン/角度との関連〜』を参照してください。

このように、\(\mathbf{a}\)と\(\mathbf{b}\)の内積は、その符号により、\(\mathbf{a}\)と\(\mathbf{b}\)がどのような「方向関係」にあるのかを表します。
これをもとにすると、\(\mathbf{a}\cdot \mathbf{b} = 0\)、つまり、\(\mathbf{a},\;\mathbf{b}\)が直交しているとは、\(\mathbf{a}\)と\(\mathbf{b}\)が「同じ」方向でも「反対」方向でもない、言うなれば「完全に無関係」な2つのベクトルという解釈ができます。
このとき、\(\mathbf{a}\)と\(\mathbf{b}\)の間の角度を\(\theta\)とすれば、\(\theta = \pi/2\)で、幾何学的に\(\mathbf{a},\;\mathbf{b}\)は直角です。
また、\(\mathbf{b}\)が正規化されていると仮定して、\(\mathbf{b}\)に沿う\(\mathbf{a}\)の射影として捉えれば、\(\mathbf{b}\)に沿う\(\mathbf{a}\)の成分が0であり、「\(\mathbf{a}\)は\(\mathbf{b}\)に対して一切の影響力がない/寄与していない」という解釈ができます。内積と射影に関しては『内積と射影の関係とは? 〜正規化された方向ベクトルを用いた内積とその解釈・応用例〜』で詳細に解説しています。
さらに、線形代数の視点で解釈すれば、「\(\mathbf{a}\)と\(\mathbf{b}\)は最も強力な線形独立関係にある」もと言えるでしょう。
以上のように、\(\mathbf{a}\cdot \mathbf{b} = 0\)として定義される\(\mathbf{a}\)と\(\mathbf{b}\)の直交関係とは、
- 幾何学的には、\(\mathbf{a}\)と\(\mathbf{b}\)が直角に交わっていて、
- 実質的な解釈としては「\(\mathbf{a}\)と\(\mathbf{b}\)が(線形的に)全く関係・関連がない」
ということになります。
「直交」とピタゴラスの定理
2つのベクトルの直交と表裏一体なのが、中学や高校でもお馴染みのピタゴラスの定理(三平方の定理)です。
このセクションでは、まず「直交」と「ピタゴラスの定理」が同値(必要十分条件)であることを確認します。
その上で、「2次多項式内での内積」、別の言い方をすれば、「相互作用項としての内積」に注目して、これまでとはやや異なった視点から内積と直交の意味を考えていきます。
「直交」の必要十分条件
2つの異なるベクトル\(\mathbf{a},\;\mathbf{b}\)から、以下の図のように\(\mathbf{a} + \mathbf{b}\)というベクトルを構成し、このベクトルのノルムの2乗\(\|\mathbf{a}+\mathbf{b}\|^2\)を考えます。
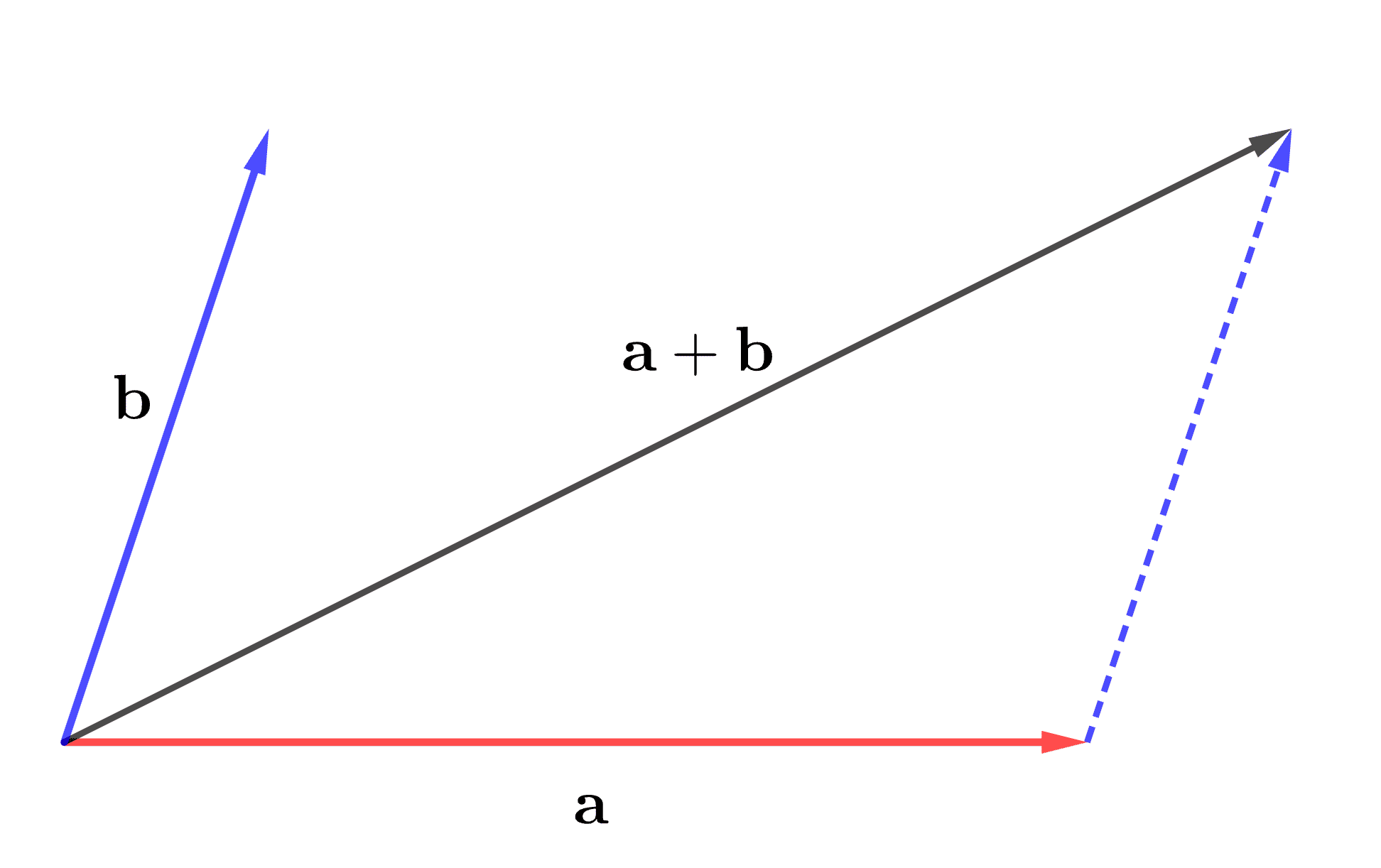
\(\|\mathbf{a}+\mathbf{b}\|^2\)に対して、ノルムの定義と内積の性質に従って展開すると、
\begin{align}
\|\mathbf{a}+\mathbf{b}\|^2 &= (\mathbf{a} + \mathbf{b}) \cdot (\mathbf{a} + \mathbf{b}) \\
&= \mathbf{a} \cdot \mathbf{a} + 2\,\mathbf{a} \cdot \mathbf{b} + \mathbf{b} \cdot \mathbf{b} \\
&= \|\mathbf{a}\|^2 + 2\,\mathbf{a} \cdot \mathbf{b} + \|\mathbf{b}\|^2
\end{align}
となります。ここで、\(\mathbf{a},\mathbf{b}\)が直交していると仮定すれば、\(\mathbf{a}\cdot \mathbf{b}=0\)なので、右辺\(2\,\mathbf{a}\cdot \mathbf{b}=0\)となり、
\[\|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\]
です。以下の図のように、この関係式は、\(\mathbf{a}\)と\(\mathbf{b}\)のノルムの間にピタゴラスの定理(三平方の定理)が成り立っていることを示しています。
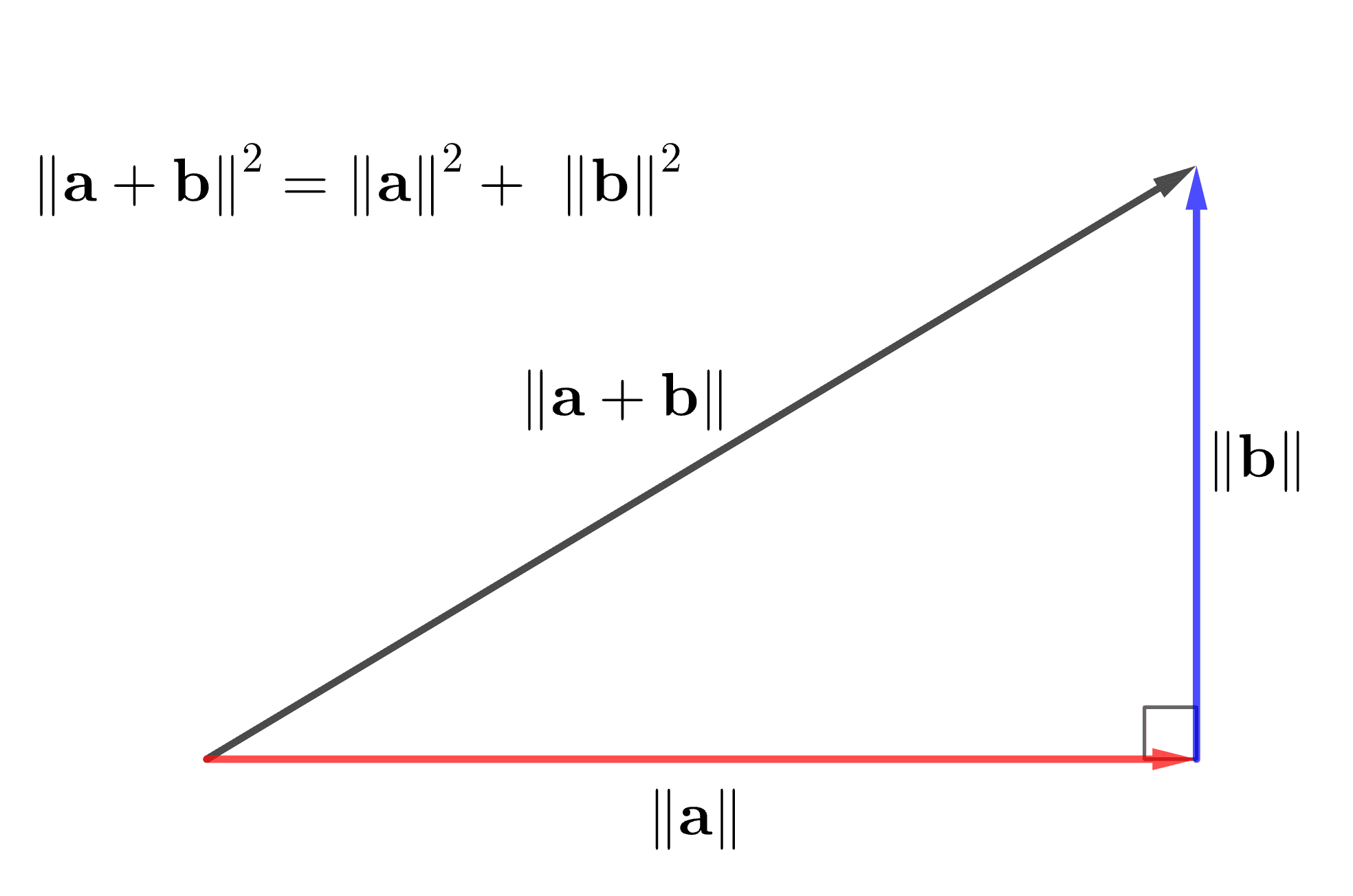
また、この逆も成り立ち、以下のように定理としてまとめることができます。
\(\mathbf{a},\mathbf{b}\)を任意の異なる2つのベクトルとする。このとき、\(\mathbf{a}\)と\(\mathbf{b}\)が直交することの必要十分条件は
\[\|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\]
が成り立つことである。
証明に関しては、「必要性」は先の解説そのものなので、「十分性」の証明のみを行います。
2つのベクトル\(\mathbf{a},\mathbf{b}\)に関して、\(\|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\)が成り立つと仮定する。このとき、左辺を展開すれば、
\[ \|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + 2\,\mathbf{a} \cdot \mathbf{b} + \|\mathbf{b}\|^2\]
である。仮定より\(\|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\)だから、\(2\,\mathbf{a} \cdot \mathbf{b} = 0\)、すなわち、
\[\mathbf{a} \cdot \mathbf{b} = 0\]
であり、\(\mathbf{a}\)と\(\mathbf{b}\)は直交している。
2次多項式での「相互作用項」としての内積
今見たように、2つのベクトル\(\mathbf{a},\mathbf{b}\)から構成される\(\mathbf{a}+\mathbf{b}\)というベクトルのノルムの二乗は、
\[ \|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + 2\,\mathbf{a} \cdot \mathbf{b} + \|\mathbf{b}\|^2\]
と展開され、その実態は2次の多項式です。\(\mathbf{a}+\mathbf{b}\)は、\(\mathbf{a}\)と\(\mathbf{b}\)の和であり、「\(\mathbf{a}\)と\(\mathbf{b}\)が混じり合った」ベクトルです。上の等式は、\(\|\mathbf{a}+\mathbf{b}\|^2\)が3つの要素\(\|\mathbf{a}\|^2\)と\(2\,\mathbf{a} \cdot \mathbf{b}\)と\(\|\mathbf{b}\|^2\)で構成されていることを主張しています。
ここで注目すべきは、内積\(\mathbf{a} \cdot \mathbf{b}\)であり、\(\|\mathbf{a}+\mathbf{b}\|^2\)の構成要素には、当然ながら\(\mathbf{a}\)と\(\mathbf{b}\)の相互作用(方向関係とその度合い)も加味されているということです。
すなわち、2次多項式\(\|\mathbf{a}+\mathbf{b}\|^2\)の展開式での内積\(\mathbf{a} \cdot \mathbf{b}\)とは、\(\mathbf{a}\)と\(\mathbf{b}\)の相互の影響・関連度合いを表した「相互作用項」としての役割を果たしている、ということです。
このとき、\(\mathbf{a}\)と\(\mathbf{b}\)の相互作用が一切ない、つまり、\(\mathbf{a}\)と\(\mathbf{b}\)が直交していると\(\mathbf{a}\cdot \mathbf{b}=0\)より、
\[ \|\mathbf{a}+\mathbf{b}\|^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2\]
となり、\( \|\mathbf{a}+\mathbf{b}\|^2\)を、相互作用項\(\mathbf{a}\cdot \mathbf{b}\)を無視して、2つの互いに無関係(独立)な成分\(\|\mathbf{a}\|^2\)と\(\|\mathbf{b}\|^2\)のみに分解できる、というわけです。
平均二乗誤差(MSE)のバイアス・バリアンス分解
データ分析・統計解析における平均二乗誤差(MSE)のバイアス・バリアンス分解は、ここまでの説明をそのまま適用している格好の例です。
平均二乗誤差(Mean Squared Error: MSE)
今、ある工場で製造しているある製品のn個の寸法データ\(x_1,x_2,\cdots,x_n\)があるとします。また、製品の寸法には望ましいとされる「基準値」があるはずのなので、その基準値をある実数値\(a\)とします。
製品の製造においては、どうしても「誤差」が生じます。つまり、実寸法\(x_i\)と基準値\(a\)がピッタリ一致することは稀で、基本的には\(+\)か\(-\)のどちらかにズレてしまいます。このような製品\(i\)の実寸法\(x_i\)の基準値\(a\)からの誤差を\(x_i – a\)で表しましょう。
誤差\(x_i-a\)は\(+\)であれ\(-\)であれ、可能な限り小さい方がよく、\(n\)個の全ての製品としてもなるべく小さくしたい。こうした動機のもと、\(n\)個の実寸法データ\(x_1,x_2,\cdots,x_n\)全体の基準値\(a\)からの誤差の大きさを評価するための統計指標として「平均二乗誤差(Mean Squared Error:MSE)」があります。
\[MSE := \sum_{i=1}^n (x_i – a)^2\]
なお、MSEの厳密な定義は確率論の期待値を用いて定義されるため、ここで今紹介した定義とは異なります。
しかし、これから説明する「誤差\(x_i-a\)をベクトル(の成分)として捉えて、このベクトルのノルムの2乗を独立した2つの成分(バイアスとバリアンス)に分解する」ということを理解する上では厳密な定義でやるとややこしくなり本質が見えづらくなるので、ここではMSEの本質は押さえつつも、細部を端折った形で導入します。
それでは、MSEをベクトル理論の土俵に乗せ、MSEにピタゴラスの定理を適用していきます。つまり、MSEをバイアスの2乗とバリアンスという2つの独立した2成分に分解していきます。
ピタゴラスの定理の観点からみる「MSEのバイアス・バリアンス分解」
まずは、誤差ベクトル\(\acute{\mathbf{x}}\)を以下のように定めます。
\[\acute{\mathbf{x}} = \begin{pmatrix}
x_1 – a \\
x_2 – a \\
\vdots \\
x_n – a
\end{pmatrix}\]
\(\acute{\mathbf{x}}\)は、n個の製品の基準値からのズレを成分にもつn次元ベクトルです。『多変量データの行列・ベクトル表現と導出 〜多変量データ行列から分散共分散行列まで〜』で解説している平均偏差ベクトルとその本質は同じです。このとき、\(\acute{\mathbf{x}}\)のノルムの2乗\(\|\acute{\mathbf{x}}\|^2\)がMSEに対応します。
\[\|\acute{\mathbf{x}}\|^2 = \sum_{i=1}^n (x_i – a)^2\]
よって、\(\|\acute{\mathbf{x}}\|^2\)を展開できて、
\begin{align}
\|\acute{\mathbf{x}}\|^2 &= \sum_{i=1}^n (x_i – a)^2 \\
&= \sum_{i=1}^n \{(x_i – \bar{x}) + (\bar{x} – a)\}^2 \\
&= \sum_{i=1}^n (x_i – \bar{x})^2 + 2\sum_{i=1}^n(x_i – \bar{x})(\bar{x} – a) + \sum_{i=1}^n(\bar{x}-a)^2 \\
&= \|\acute{\mathbf{x}_v}\|^2 + 2\acute{\mathbf{x}_v} \cdot \acute{\mathbf{x}_b} + \|\acute{\mathbf{x}_b}\|^2
\end{align}
となります。ここで、\(\bar{x}\)は、実寸法データの標本平均
\[\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\]
です。また、
\[\|\acute{\mathbf{x}_v}\|^2 = \sum_{i=1}^n (x_i – \bar{x})^2\]
としましたが、これは、
\[\acute{\mathbf{x}_v} = \begin{pmatrix}
x_1 – \bar{x} \\
x_2 – \bar{x} \\
\vdots \\
x_n – \bar{x}
\end{pmatrix}\]
という実寸法データ\(x_1,x_2,\cdots,x_n\)の標本平均からの偏差積和を成分とするベクトルのノルムの2乗であり、その本質は、(標本)分散(variance/バリアンス)です(厳密には\(n\)で割っていないので分散ではありません)。
つまり、\(\|\acute{\mathbf{x}_v}\|^2\)は、寸法データ\(x_1,x_2,\cdots,x_n\)の標本平均\(\bar{x}\)周りでのバラツキの大きさを表し、これをバリアンス項と言います。
一方で、もう1つは
\[\|\acute{\mathbf{x}_b}\|^2 = \sum_{i=1}^n(\bar{x}-a)^2\]
ですが、こちらは、
\[\acute{\mathbf{x}_b} = \begin{pmatrix}
\bar{x}-a \\
\bar{x}-a \\
\vdots \\
\bar{x}-a
\end{pmatrix}\]
というように、n個の\((\bar{x}-a)\)を成分とするベクトルのノルムの2乗です。\((\bar{x}-a)\)は「バイアス(bias)」という指標であり、\(\|\acute{\mathbf{x}_b}\|^2\)は、実寸法データの標本平均\(\bar{x}\)の基準値\(a\)からのバラツキの大きさ(の2乗)を表し、こちらをバイアス項といいます。さらに、
\[\acute{\mathbf{x}_v} \cdot \acute{\mathbf{x}_b}=0\]
です。つまり、バリアンスベクトル\(\acute{\mathbf{x}_v}\)とバイアスベクトル\(\acute{\mathbf{x}_b}\)は直交します。なぜならば、
\begin{align}
\acute{\mathbf{x}_v} \cdot \acute{\mathbf{x}_b} &= \sum_{i=1}^n(x_i – \bar{x})(\bar{x} – a) \\
&= (\bar{x} – a)\sum_{i=1}^n(x_i – \bar{x}) \\
&= (\bar{x} – a)\left (\sum_{i=1}^n x_i – \sum_{i=1}^n \bar{x}\right)\\
&= (\bar{x} – a) (n\bar{x}-n\bar{x}) \\
&= 0
\end{align}
だからです。従って、MSEの展開式における相互作用項\(\acute{\mathbf{x}_v} \cdot \acute{\mathbf{x}_b}\)は消え去り、
\[MSE = \|\acute{\mathbf{x}_v}\|^2 + \|\acute{\mathbf{x}_b}\|^2\]
という分解が成り立ちます。これをMSEのバイアス・バリアンス分解といいます。以下はイメージ図です。
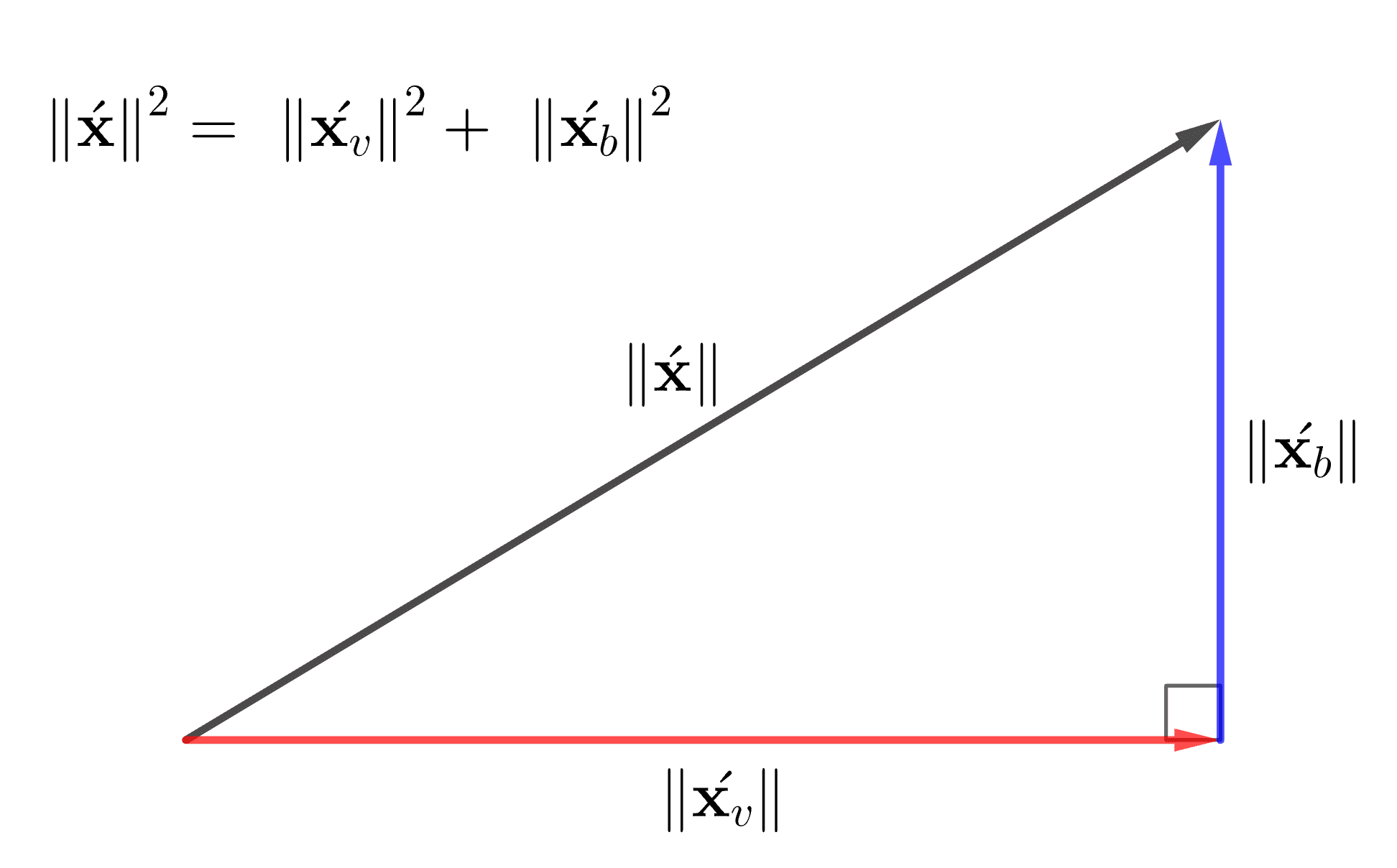
基準値\( a\) からの誤差\( x_i – a\) の二乗和(MSE)を
- \( \|\acute{\mathbf{x}_v}\|^2\): 個々のデータの標本平均周りでのバラツキ(バリアンス)
- \( \|\acute{\mathbf{x}_b}\|^2\): 個々のデータから算出した標本平均\(\bar{x}\)の基準値からのバラツキ(バイアスの2乗)
という独立した2つのバラツキ成分に分解することで、誤差(MSE)のより詳細な分析が可能になります。
こうした分解は統計学やデータ解析理論を勉強しているとしばしば現れ、例えば、実験計画法における分散分析で、分散を群間変動と群内変動に分解するのが挙げられます。
なお、本題からはやや逸れますが、『NOISE: 組織はなぜ判断を誤るのか?』という本では、一流の研究者が、どのようにバイアス・バリアンス分解を使って誤差(MSE)を解析するのか、その一端を学ぶことができます。
本書では、人間の「判断誤差」を「バイアス」と「ノイズ(バリアンス)」に分解します。その上で、一般的に知られるようになったバイアスはほどほどに、ほとんど無視されている(知られていない)ノイズに焦点を当て、「ノイズが大きくの組織や社会をいかに蝕んでいるか」を説明しています。
参考文献
本記事を執筆するにあたり参考にした書籍・教材は以下の通りです。
なお、参考文献や教材の紹介にあたっては、アフィリエイトリンクを貼っていることをご承知ください。
線形代数の理論とPythonによる実践

線形代数の理論とPythonによる実践は、本ではなくUdemyの動画教材です。
本記事では、直交とピタゴラスの定理の同値性とその証明方法に関して参考にしました。
プログラミングのための確率統計
MSEのバイアス・バリアンス分解の統計解析的な観点は本書を参考にしました。
確率論と数理統計学の結構深い内容を、厳密さを犠牲にする代わりに、分かりやすさと直感的な理解に重点を置いた参考書です。
はじめてのパターン認識
MSEをバイアス項とバリアンス項に分解する際の式変形は本書を参考にしました。
基本的な機械学習手法の理論面を初心者向けに丁寧に解説している本です。



